Ш¬ШіШӘШ§Шұ
ЪҶЫҢШіШӘШ§ЩҶвҖҢЩҮШ§ ЩҲ ШҙШ№ШЁШҜЩҮвҖҢЩҮШ§ЫҢ ШұЫҢШ§Ш¶ЫҢ ШҜШұ Ъ©ШӘШ§ШЁ ШӘШӯЩҒШ©Ш§Щ„ШәШұШ§ШҰШЁ
- Ш¬ШіШӘШ§Шұ
- ЩҶЩ…Ш§ЫҢШҙ Ш§ШІ ШҙЩҶШЁЩҮ, 19 ШҜЫҢ 1394 04:39
ШҜЪ©ШӘШұ Щ…ШӯЩ…ШҜШұШ¶Ш§ ШӘЩҲЪ©Щ„ЫҢ ШөШ§ШЁШұЫҢ
Щ…Ш№ШұЩҒЫҢ Ъ©ШӘШ§ШЁ В«ШӘШӯЩҒШ© Ш§Щ„ШәШұШ§ШҰШЁВ»
ШӘШӯЩҒЩҮ Ш§Щ„ШәШұШ§ШҰШЁ* Ъ©ШӘШ§ШЁЫҢ Ш§ШіШӘ Ъ©ЩҮ ШҜШұ ЩӮШұЩҶ ЩҫЩҶШ¬Щ… ЩҮШ¬ШұЫҢ ЩҶЩҲШҙШӘЩҮ ШҙШҜЩҮ Ш§ШіШӘ. ШӘШ§ШұЫҢШ® ШӘШ§Щ„ЫҢЩҒ ШўЩҶ ШҜШұ Щ…ЩҶШ§ШЁШ№ Щ…Ш®ШӘЩ„ЩҒ ШЁЫҢЩҶ ШіШ§Щ„ ЩЈЫөЫҙ ШӘШ§ ЫөЩЎЩЈ ЩҮШ¬ШұЫҢ ЩӮЩ…ШұЫҢ ШўЩ…ШҜЩҮ Ш§ШіШӘШҢ Ш§Щ…Ш§ Щ…ШөШӯШӯ Ъ©ШӘШ§ШЁ ШўЩҶ ШұШ§ ШҜШұ ШӯШҜЩҲШҜ ШіШ§Щ„ ЫҙЩЁЫө Щ…ЫҢвҖҢШҜШ§ЩҶШҜ. Ш§ЫҢЩҶ Ъ©ШӘШ§ШЁ ЫҢЪ© ШҜШ§ШҰШұШ©Ш§Щ„Щ…Ш№Ш§ШұЩҒ Ш№Щ„Щ…ЫҢ ШІЩ…Ш§ЩҶ Ш®ЩҲШҜШҙ Ш§ШіШӘ. Ш§ЫҢЩҶ Ш§Ш·Щ„Ш§Ш№Ш§ШӘ ШЁЩҮШӘШұЫҢЩҶ ЩҲ Ш№Щ„Щ…ЫҢвҖҢШӘШұЫҢЩҶ ЩҶЩҲШ№ Ш§Ш·Щ„Ш§Ш№Ш§ШӘ ШӘШ§ ШІЩ…Ш§ЩҶ Ш®ЩҲШҜШҙ ШЁЩҲШҜЩҮ Ш§ШіШӘ. ЩҒШөЩ„ ШЁЫҢШіШӘЩ…В ШӘШӯЩҒШ©Ш§Щ„ШәШұШ§ШҰШЁ ШҜШұ Щ…ЩҲШұШҜ Щ…ШіШ§ЫҢЩ„ ШұЫҢШ§Ш¶ЫҢШҢ ЩҮЩҶШҜШіЫҢ ЩҲ Ш¬ШЁШұЫҢШҢ ЪҶЫҢШіШӘШ§ЩҶвҖҢЩҮШ§ШҢ ШіШұЪҜШұЩ…ЫҢвҖҢЩҮШ§ШҢ ЩҲ ШҙШ№ШЁШҜЩҮвҖҢЩҮШ§ЫҢ ШұЫҢШ§Ш¶ЫҢ Ш§ШіШӘ Ъ©ЩҮВ ШҜШұ Щ…Ш¬Ш§Щ„Ші ЩҲ Щ…ШӯШ§ЩҒЩ„ ШўЩҶ ШІЩ…Ш§ЩҶ ШЁЩҮ Ъ©Ш§Шұ Щ…ЫҢвҖҢШұЩҒШӘЩҮ Ш§ШіШӘ. Ш§ЫҢЩҶ ЩҒШөЩ„ ШіШ·Шӯ Ш¬ШҜЫҢвҖҢШӘШұЫҢЩҶ ШҜШ§ЩҶШҙ ШЁШҙШұЫҢ ЫҢШ№ЩҶЫҢ ШұЫҢШ§Ш¶ЫҢШ§ШӘ Ъ©Ш§ШұШЁШұШҜЫҢ ШұШ§ ШҜШұ Ш§ЫҢШұШ§ЩҶ ЩҶШҙШ§ЩҶ Щ…ЫҢвҖҢШҜЩҮШҜ.
Ш№Щ„Ш§ЩҲЩҮ ШЁШұ Ш§ЩҮЩ…ЫҢШӘ ШўЩҶ ШЁЩҮ Ш№ЩҶЩҲШ§ЩҶ ЫҢЪ© Ъ©ШӘШ§ШЁ Ш№Щ„Щ…ЫҢ Ш§ЫҢШұШ§ЩҶЫҢШҢ Ш§ШІ ЩҶШёШұ Ш¬ЩҮШ§ЩҶЫҢ Ш§ЩҮЩ…ЫҢШӘ ШўЩҶ Ш§ШІ ЩҶШёШұ ШӘШ§ШұЫҢШ® ШҙШ№ШЁШҜЩҮ ШЁШ§ШІЫҢ Ш§ШіШӘ. ЩӮШҜЫҢЩ…ЫҢ ШӘШұЫҢЩҶ Ъ©ШӘШ§ШЁЫҢ Ъ©ЩҮ ШҜШұ ШЁШ§ШұЩҮ ШҙШ№ШЁШҜЩҮ ШЁШ§ШІЫҢ ЩҶЩҲШҙШӘЩҮ ШҙШҜЩҮ Ш§ШіШӘ ШӘЩҲШіШ· Ъ©ШҙЫҢШҙЫҢ ЩҒШұШ§ЩҶШіЫҢШіЪ©ЩҶ ШЁЩҮ ЩҶШ§Щ… Щ„ЩҲЪ©Ш§ ЩҫШ§ЪҶЫҢЩҲЩ„ЫҢ ШҜШұ ШЁЫҢЩҶ ШіШ§Щ„ЩҮШ§ЫҢ ЩЎЫҙЩ©Ы¶ ЩҲ ЩЎЫөЩ ЩЁ ЩҶЩҲШҙШӘЩҮ ШҙШҜЩҮ Ш§ШіШӘ. Ш§ЩҮЩ…ЫҢШӘ Ъ©ШӘШ§ШЁ Ш·ШЁШұЫҢ Ш§ЫҢЩҶ Ш§ШіШӘ Ъ©ЩҮ ШӘШ§ШұЫҢШ® ШҙШ№ШЁШҜЩҮ ШЁШ§ШІЫҢ ШұШ§ ШіШұ ЩҲ ШӘЩҮ Щ…ЫҢвҖҢЪ©ЩҶШҜ. ШІЫҢШұШ§ Ш§ЫҢЩҶ ШӘШ§ШұЫҢШ® ШұШ§ ШҜШұ ШӯШҜЩҲШҜ ЩҫШ§ЩҶШөШҜ ШіШ§Щ„ ШЁЩҮ Ш№ЩӮШЁ Щ…ЫҢвҖҢШЁШұШҜ ЩҲ Ш§ЫҢЩҶ Ш§ЩҒШӘШ®Ш§Шұ ШЁШІШұЪҜЫҢ ШЁШұШ§ЫҢ Ш§ЫҢШұШ§ЩҶЫҢШ§ЩҶ Ш§ШіШӘ.
Ш§ШІ ШўЩҶШ¬Ш§ЫҢЫҢ Ъ©ЩҮ Ш§ЫҢЩҶ Ъ©ШӘШ§ШЁ ШҜШұ Ш·ЫҢ ЩҮШІШ§Шұ ШіШ§Щ„ ШӘЩҲШіШ· ЩҶШіШ®ЩҮ ШЁШұШҜШ§ШұШ§ЩҶЫҢ Ъ©ЩҮ ШҙШ§ЫҢШҜ ШіЩҲШ§ШҜ Ш®ЩҲШ§ЩҶШҜЩҶ Ъ©Щ…ЫҢ ШҜШ§ШҙШӘЩҮ Ш§ЩҶШҜ ЩҲ ШЁЩҮ Щ…ЩҲШ¶ЩҲШ№Ш§ШӘ ШұЫҢШ§Ш¶ЫҢ ШўШҙЩҶШ§ЫҢЫҢ ЩҶШҜШ§ШҙШӘЩҮ Ш§ЩҶШҜ ЩҶЩҲШҙШӘЩҮ ШҙШҜЩҮ Ш§ШіШӘ ЩҲ Ш§ШөШ·Щ„Ш§ШӯШ§ШӘ ЩӮШҜЫҢЩ…ЫҢ ШҜШұ ШўЩҶ ШЁЩҮ Ъ©Ш§Шұ ШұЩҒШӘЩҮ Ш§ШіШӘШҢ Щ…Щ…Ъ©ЩҶ Ш§ШіШӘ ШЁШұШ§ЫҢ ЩҮЩ…ЪҜШ§ЩҶ ЩӮШ§ШЁЩ„ ЩҒЩҮЩ… ЩҶШЁШ§ШҙШҜ. ШҜШұ ШІЫҢШұ Щ…Ш§ Щ…ШӘЩҶ Щ…ШіШ§ЫҢЩ„ ЩҲ ШұШ§ЩҮ ШӯЩ„ ШўЩҶЩҮШ§ ШұШ§ Ш§ШІ Ъ©ШӘШ§ШЁ ШӘШӯЩҒЩҮ Ш§Щ„ШәШұШ§ШҰШЁ ЩҶЩӮЩ„ Ъ©ШұШҜЩҮ ЩҲ ШіЩҫШі ШЁЩҮ Ш§ШұШ§ШҰЩҮ ШұШ§ЩҮ ШӯЩ„ ШўЩҶЩҮШ§ Щ…ЫҢ ЩҫШұШҜШ§ШІЫҢЩ….
В
ШЁШ§ШЁ ШЁЫҢШіШӘЩ… ШҜШұ ЩҶЩ…ЩҲШҜЩҶ ШЁШ§ШІЫҢЩҮШ§ЫҢ ЪҶШ§ШЁЪ© Щ„Ш·ЫҢЩҒ ЩҲ Щ…Ш¬Щ„ШівҖҢЩҮШ§ ЩҲ Ш¬Ш§ЫҢвҖҢЩҮШ§
ЩҲ Ш§ЪҜШұ Ш®ЩҲШ§ЩҮЫҢ Ъ©ЩҮ ЪҶЩҲЩҶ Ш¬Щ…Ш№ЫҢ Ш¬Ш§ЫҢЫҢ ШӯШ§Ш¶Шұ ШўЩ…ШҜЩҮ ШЁШ§ШҙЩҶШҜ ЩҲ Ш®ЩҲШ§ЩҮЩҶШҜ Ъ©ЩҮ Щ„Ш№ШЁЩҮвҖҢШ§ЫҢ ЪҶШ§ШЁЪ© ЩҶЩ…Ш§ЫҢЩҶШҜ ШЁЩҮ ШҙЩ…Ш§ШұЩҮШ§ШҢ ЩҲШ¬ЩҮЫҢ ЪҶЩҶШҜ Ш§ЩҶШҜШұ Ш§ЫҢЩҶ ШЁШ§ШЁ ЫҢШ§ШҜ Ъ©ЩҶЫҢЩ…:
ЪҶЩҲЩҶ Ш§ЩҶЪҜШҙШӘШұЫҢ ЫҢШ§ ЪҶЫҢШІЫҢ ШҜЫҢЪҜШұ ШҜШұ Щ…ЫҢШ§ЩҶ ЩӮЩҲЩ…ЫҢ ЩҫЩҶЩҮШ§ЩҶ Ъ©ШұШҜЩҮ ШЁШ§ШҙЩҶШҜ ЩҲ Ш®ЩҲШ§ЩҮЩҶШҜ Ъ©ЩҮ ЩҫЫҢШҜШ§ Ъ©ЩҶЩҶШҜ Ъ©ЩҮ Ъ©ШҜШ§Щ… Ъ©Ші ШҜШ§ШұШҜШҢ ШЁШ§ЫҢШҜ Ъ©ЩҮ ЫҢЪ©ЫҢ ШұШ§ ШЁЩҒШұЩ…Ш§ЫҢЩҶШҜ ШӘШ§ ШҜШұ ШҜЩ„ Ш®ЩҲЫҢШҙ Ъ©ШұШҜ Ш§ШІ ШҜШіШӘ ШұШ§ШіШӘ ШўЩҶ Ъ©Ші ШӘШ§ ШўЩҶШ¬Ш§ Ъ©ЩҮ Ш§ЩҶЪҜШҙШӘШұЫҢ ШҜШ§ШұШҜ ШЁШҙЩ…Ш§ШұШҜШҢ ЪҶЩҲЩҶ ШҙЩ…ШұШҜЩҮ ШЁШ§ШҙЩҶШҜШҢ ЪҜЩҲЫҢШҜ Ъ©ЩҮВ ЩҶЫҢЩ…ЩҮ ШўЩҶ ШЁШұ ЩҲЫҢ Ш§ЩҒШІШ§ЫҢ. ЪҶЩҲЩҶ Ш§ЩҒШІЩҲШҜШҢ ШЁЩҫШұШіШҜ Ъ©ЩҮ: ШўЩҶ ШӯШ§ШөЩ„ Ъ©ШіЩҲШұ Ш§ЩҒШӘШ§ШҜШҢ ЫҢШ№ЩҶЫҢ ЩҶЫҢЩ…ЩҮ ШўЩҶ Ш§ЩҒШӘШ§ШҜШҢ ЫҢЪ© Ш№ШҜШҜ ЩҶЪҜШ§ЩҮ ШҜШ§ШұШҜ. ЩҲ Ш§ЪҜШұ ЪҜЩҲЫҢШҜ: ЩҮЫҢЪҶ ЩҶЫҢЩҒШӘШ§ШҜШҢ ЩҶЪҜШ§ЩҮ ЩҶШҜШ§ШұШҜ ЩҲ ШўЩҶ ЫҢЪ© Ш№ШҜШҜ ЩҫШі Ш§ЪҜШұ Ш§ЩҒШӘШ§ШҜЩҮ ШЁЩҲШҜШҢ ЩҶЫҢЩ… ШҜШұЩ… ШЁШұ ЩҲЫҢ ЩҶЩҮ ШӘШ§ ШӘЩ…Ш§Щ… ШҙЩҲШҜ. ЪҶЩҲЩҶ ШӘЩ…Ш§Щ… Ъ©ШұШҜЩҮ ШЁШ§ШҙШҜШҢ ШЁШ§ШІ ЪҜЩҲЫҢШҜ: ШҜЩҲЩ… ШЁШ§Шұ Ъ©ЩҮ ЩҶЫҢЩ…ЩҮ ШўЩҶ Щ…ШЁЩ„Шә ШЁШұ ЩҲЫҢ Ш§ЩҒШІШ§ЫҢ. ЪҶЩҲЩҶ ШЁШұШ§ЩҒШІЩҲШҜШҢ ШЁЩҫШұШіШҜ Ъ©ЩҮ:В ШҜШұ ЩҲЫҢ Ъ©ШіЩҲШұ Ш§ЩҒШӘШ§ШҜ ЫҢШ§ ЩҶЩҮШҹ Ш§ЪҜШұ ЪҜЩҲЫҢШҜ Ъ©ЩҮ Ш§ЩҒШӘШ§ШҜШҢ Ш№ШҜШҜ ШҜЫҢЪҜШұ ШЁШұ ШўЩҶ ЫҢЪ© Ш№ШҜШҜ ЩҶЪҜШ§ЩҮ ШҜШ§ШҙШӘЩҮ Ш§ЩҒШІШ§ЫҢ. Ш§ЪҜШұ ЫҢЪ© ШҜШ§ШҙШӘЩҮ ШЁШ§ШҙЫҢ ЩҲ Ш§ЪҜШұ ЩҶШҜШ§ШҙШӘЩҮ ШЁШ§ШҙЫҢШҢ Ш§ЫҢЩҶ ШҜЩҲ ЩҶЪҜШ§ЩҮ ШҜШ§Шұ ЩҲ ШЁЪҜЩҲ ШўЩҶ Ъ©Ші ШұШ§ Ъ©ЩҮ: Ъ©ШіЩҲШұ ШӘЩ…Ш§Щ… Ъ©ЩҶ. ЪҶЩҲЩҶ ШӘЩ…Ш§Щ… Ъ©ШұШҜШҢ ЪҜЩҲЫҢШҜ Ъ©ЩҮ: ЩҶЩҮ Ш§ШІ ЩҲЫҢ ШЁШұЩҲ. ЪҶЩҲЩҶ ШЁШұЩҒШӘ ШЁЪҜЩҲ:В ЩҶЩҮ ШҜЫҢЪҜШұ ШЁШұЩҲШҜ. ЩҮЩ…ЪҶЩҶШ§ЩҶ ЩҶЩҮ ЩҶЩҮ Ш§ШІ ЩҲЫҢ ЩҮЩ…ЫҢ ШұЩҲШҜ ШӘШ§ ШўЩҶ ШіШ§Ш№ШӘ Ъ©ЩҮ ШҜШұ Ш§ЩҲ ЩҶЩҮ ЩҶШЁШ§ШҙШҜ ЩҲ ШЁЩҮ ЩҮШұ ЩҶЩҮЫҢ Ъ©ЩҮ ШұЩҒШӘЩҮ ШЁШ§ШҙШҜ ЪҶЩҮШ§Шұ Ш№ШҜШҜ ШЁШұ ШўЩҶ Ш№ШҜШҜ ЩҶЪҜШ§ЩҮ ШҜШ§ШҙШӘЩҮ ЩҮЩ…ЫҢ Ш§ЩҒШІШ§ЫҢШҜШҢ Ш§ЪҜШұ ШҜШ§ШұШҜ ЩҲ Ш§ЪҜШұ ЩҶШҜШ§ШұШҜШҢ ЪҶЩҮШ§Шұ ЪҶЩҮШ§Шұ ЩҶЪҜШ§ЩҮ ЩҮЩ…ЫҢ ШҜШ§ШұШҜШҢ ЩҲ ШўЩҶЪҜЩҮ ШЁШЁЫҢЩҶШҜ Ъ©ЩҮ ЪҶЩҮ ШӯШ§ШөЩ„ ШўЩ…ШҜЩҮ Ш§ШіШӘ. ШўЩҶЪҶЩҮ ШўЩ…ШҜЩҮ ШЁШ§ШҙШҜ Ш§ШІ ШҜШіШӘ ШұШ§ШіШӘ ШўЩҶ Щ…ШұШҜ ШЁШҙЩ…Ш§ШұШҜ ШӘШ§ ШўЩҶШ¬Ш§ Ъ©ЩҮ ШЁШұШ§ЩҒШӘШҜ Ш§ЩҶЪҜШҙШӘШұЫҢ ШЁШіШӘШ§ЩҶШҜ.
Щ…Ш«Ш§Щ„Шҙ: ЪҶЩҶШ§ЩҶ Ъ©ЩҮ Ш§ЪҜШұ ШҜШұ Щ…Ш¬Щ„Ші ЩҫШ§ЩҶШІШҜЩҮ Ъ©Ші ШӯШ§Ш¶Шұ ШЁШ§ШҙЩҶШҜШҢ ЫҢЪ©ЫҢ Ш§ШІ Ш§ЫҢШҙШ§ЩҶ Ш§ЩҶЪҜШҙШӘШұЫҢ ЩҫЩҶЩҮШ§ЩҶ Ъ©ШұШҜЩҮШҢ ЩҲ ЩҮЩҒШӘЩ… Ъ©Ші ШҜШ§ШұШҜ ЩҲ Щ…ЫҢШ§ЩҶ ШўЩҶ ЪҜШұЩҲЩҮ Ъ©Ші ШұШ§ Щ…Ш№Щ„ЩҲЩ… ЩҶЫҢШіШӘ Ъ©ЩҮ ШўЩҶ Ш§ЩҶЪҜШҙШӘШұЫҢ Ъ©ЩҮ ШҜШ§ШұШҜ Щ…ЪҜШұ ШўЩҶ Ъ©Ші Ъ©ЩҮ Ш§ЩҶЪҜШҙШӘШұЫҢ ЩҫЩҶЩҮШ§ЩҶ Ъ©ШұШҜ.В ЩҫШі ЪҜЩҒШӘЩ…: ШЁШҙЩ…Ш§Шұ ШӘШ§ ШўЩҶ Ъ©Ші Ъ©ЩҮ ЪҜЩҒШӘ: ШЁШҙЩ…ШұШҜЩ…. ЪҜЩҒШӘЩ…:В ЩҶЫҢЩ…ЩҮ ЩҲЫҢ ШЁШұ ЩҲЫҢ Ш§ЩҒШІШ§ЫҢ. ЪҜЩҒШӘ: Ш§ЩҒШІЩҲШҜЩ…. ЩҫШұШіЫҢШҜЩ… Ъ©ЩҮ: Ъ©ШіЩҲШұ ЩҮШіШӘ ШҜШұ ЩҲЫҢ ЫҢШ§ ЩҶЩҮШҹ ЪҜЩҒШӘ: ЩҮШіШӘШҢ Щ…Ш§ ЫҢЪ© Ш№ШҜШҜ ЩҶЪҜШ§ЩҮ ШҜШ§ШҙШӘЫҢЩ….В ЩҲ ЪҜЩҒШӘЩ…: ШўЩҶ Ъ©ШіЩҲШұ ШӘЩ…Ш§Щ… Ъ©ЩҶ. ЪҜЩҒШӘ: Ъ©ШұШҜЩ…. ЪҜЩҒШӘЩ… ШҜЩҲ ШЁШ§Шұ ЩҶЫҢЩ…ЩҮ ЩҲЫҢ ШЁШұ ЩҲЫҢ Ш§ЩҒШІШ§ЫҢ. ЪҜЩҒШӘ: Ш§ЩҒШІЩҲШҜЩ…. ЪҜЩҒШӘЩ…: Ъ©ШіЩҲШұШіШӘШҹ ЪҜЩҒШӘ: ЩҮШіШӘШҢ Щ…Ш§ ШҜЩҲ Ш№ШҜШҜ ШЁШұ ШўЩҶ ЫҢЪ© Ш№ШҜШҜ ШҜЫҢЪҜШұ Ш§ЩҒШІЩҲШҜЫҢЩ… ШӘШ§ ШіЩҮ ШҙШҜ. ШўЩҶ ШіЩҮ ЩҶЪҜШ§ЩҮ ШҜШ§ШҙШӘЫҢЩ… ЩҲ ЪҜЩҒШӘЩ…: ШўЩҶ Ъ©ШіЩҲШұ ШӘЩ…Ш§Щ… Ъ©ЩҶ. ЪҜЩҒШӘ: ШӘЩ…Ш§Щ… Ъ©ШұШҜЩ…. ЪҜЩҒШӘЩ…: ЩҶЩҮ Ш§ШІ ЩҲЫҢ ШЁШұЩҲ. ЪҜЩҒШӘ: ШұЩҒШӘЩ…. Щ…Ш§ ЪҶЩҮШ§Шұ Ш№ШҜШҜ ШЁШұ ШўЩҶ ШіЩҮ Ш№ШҜШҜ ЩҶЪҜШ§ЩҮ ШҜШ§ШҙШӘЩҮ Ш§ЩҒШІЩҲШҜЫҢЩ… ШӘШ§ ЩҮЩҒШӘ ШӯШ§ШөЩ„ ШҙШҜ. ЪҜЩҒШӘЩ…: ЩҶЩҮ ШҜЫҢЪҜШұ ШЁШЁШұ. ЪҜЩҒШӘ: ЩҶЫҢШіШӘ. Щ…Ш№Щ„ЩҲЩ… ШҙШҜ Ъ©ЩҮ ЩҮЩҒШӘЩ…ЫҢЩҶ Ъ©Ші ШҜШ§ШұШҜ.
ШҜШұ Ш§ЫҢЩҶ ШҙШ№ШЁШҜЩҮ ШЁШ§ШІЫҢ Ъ©ЩҮ ШЁЩҮ ШўЩҶ ЩҫЫҢШҙвҖҢШЁЫҢЩҶЫҢ ЩҲ ЫҢШ§ ШұЩҲШҙЩҶвҖҢШЁЫҢЩҶЫҢ Щ…ЫҢ ЪҜЩҲЫҢЩҶШҜШҢ ШҜШұ Ш¬Щ…Ш№ЫҢ Ш§ШІ Ш§ЩҒШұШ§ШҜ ЫҢЪ© ЩҶЩҒШұ Ш§ЩҶЪҜШҙШӘШұЫҢВ ШұШ§ ШЁЩҮ ЫҢЪ©ЫҢ Ш§ШІ ШӯШ§Ш¶ШұЫҢЩҶ ШҜШұ ШіЩ…ШӘ ШұШ§ШіШӘ ЩҲ ЫҢШ§ ШіЩ…ШӘ ЪҶЩҫ Ш®ЩҲШҜ Щ…ЫҢ ШҜЩҮШҜ ЩҲ ШЁШҜЩҲЩҶ ШўЩҶ Ъ©ЩҮ ШЁЪҜЩҲЫҢШҜ Ъ©ЩҮ ШЁЩҮ ЩҶЩҒШұ ЪҶЩҶШҜЩ… ШҜШ§ШҜЩҮ Ш§ШіШӘ Ш§ШІ ШҙШ№ШЁШҜЩҮ Щ…ЫҢвҖҢШ®ЩҲШ§ЩҮШҜ Ш§ЩҶЪҜШҙШӘШұ ШұШ§ ЩҫЫҢШҜШ§ Ъ©ЩҶШҜ. ШҙШ№ШЁШҜЩҮ ШЁШ§ШІ Ш§ШІ ШөШ§ШӯШЁ Ш§ЩҶЪҜШҙШӘШұ Щ…ЫҢвҖҢШ®ЩҲШ§ЩҮШҜ Ъ©ЩҮ ШЁШҜЩҲЩҶ Ш§ЫҢЩҶ Ъ©ЩҮ ШЁЩҮ Ш§ЩҲ Ш§Ш№Щ„Ш§Щ… Ъ©ЩҶШҜШҢ Ш§ШІ Ш®ЩҲШҜШҙ ШӘШ§ ШҙШ®ШөЫҢ Ъ©ЩҮ Ш§ЩҶЪҜШҙШӘШұ ШұШ§ ШҜШ§ШұШҜ ШЁШҙЩ…Ш§ШұШҜ ЩҲ ЩҮШұ Ш№ШҜШҜЫҢ ШЁЩҲШҜ ЩҶЫҢЩ…ЫҢ Ш§ШІ ШўЩҶ ШұШ§ ШЁЩҮ ЩҮЩ…Ш§ЩҶ Ш№ШҜШҜ ШЁЫҢЩҒШІШ§ЫҢШҜ. ШіЩҫШі Ш§ШІ ЩҲЫҢ Щ…ЫҢШ®ЩҲШ§ЩҮШҜ Ш§ЪҜШұ Ш№ШҜШҜ Ш§Ш№ШҙШ§ШұЫҢ ШҜШұ ШўЩ…ШҜШҢ ЫҢШ№ЩҶЫҢ Ш№ШҜШҜ Ъ©Ш§Щ…Щ„ ЩҶШЁЩҲШҜШҢ ЩҶЫҢЩ…ЫҢ ШЁЩҮ ШўЩҶ ШЁЫҢШ§ЩҒШІШ§ЫҢШҜ ШӘШ§ Ш№ШҜШҜ Ъ©Ш§Щ…Щ„ ШҙЩҲШҜ. ШҜШұ Ш§ЫҢЩҶ ШӯШ§Щ„ Ш§ЪҜШұ Ш№ШҜШҜ Ш§Ш№ШҙШ§ШұЫҢ ШЁЩҲШҜШҢ ШҙШ№ШЁШҜЩҮ ШЁШ§ШІ Ш№ШҜШҜ ЫҢЪ© ШұШ§ ЩҶЪҜШ§ЩҮ Щ…ЫҢ ШҜШ§ШұШҜ ЩҲШ§ЪҜШұ Ш№ШҜШҜ Ъ©Ш§Щ…Щ„ ШЁЩҲШҜШҢ Ъ©Ш§ШұЫҢ ЩҶЩ…ЫҢЪ©ЩҶШҜ. ШіЩҫШі ШЁШұШ§ЫҢ ШЁШ§Шұ ШҜЩҲЩ… Щ…ЫҢ ЪҜЩҲЫҢШҜШҢ ШӯШ§ШөЩ„ Ш¬Щ…Ш№ ЩҮШұ Ш№ШҜШҜЫҢ ШЁЩҲШҜ ЩҶЫҢЩ… ЩҮЩ…Ш§ЩҶ Ш№ШҜШҜ ШұШ§ ШЁЩҮ Ш№ШҜШҜ ШЁЩҮ ШҜШіШӘ ШўЩ…ШҜЩҮ ШЁЫҢШ§ЩҒШІШ§ЫҢШҜ. ШЁШ№ШҜ Щ…ЫҢ ЩҫШұШіШҜ Ш№ШҜШҜ Ъ©Ш§Щ…Щ„ ШЁЩҲШҜ ЫҢШ§ Ш§Ш№ШҙШ§ШұЫҢШҢ Ш§ЪҜШұ Ш§Ш№ШҙШ§ШұЫҢ ШЁЩҲШҜ Ш№ШҜШҜ ШҜЩҲ ШұШ§ ШЁЩҮ Ш№ШҜШҜ ЫҢЪ© Щ…ЫҢвҖҢШ§ЩҒШІШ§ЫҢШҜ ЩҲ Ш§ЪҜШұ Ш№ШҜШҜ Ъ©Ш§Щ…Щ„ ШЁЩҲШҜШҢ Ъ©Ш§ШұЫҢ ЩҶЩ…ЫҢ Ъ©ЩҶШҜ. ШіЩҫШі ШЁЩҮ Ш§ЩҲ Щ…ЫҢ ЪҜЩҲЫҢШҜ Ъ©ЩҮ Ш№ШҜШҜ ЩҶЩҮ ШұШ§ Ш§ШІ ШўЩҶ Ъ©Щ… Ъ©ЩҶШҜ. Ш§ЪҜШұ Ш№ШҜШҜ Ш§ШІ ЩҶЩҮВ Ъ©Щ…ШӘШұ ШЁЩҲШҜ Ъ©Ш§ШұЫҢ ЩҶЩ…ЫҢЪ©ЩҶШҜ ЩҲ Щ…ШӯШ§ШіШЁЩҮ Ш§ЫҢЩҶШ¬Ш§ ШӘЩ…Ш§Щ… ШҙШҜЩҮ ЩҲ Ш§ШІ Ш·ШұЩҒ ШөШ§ШӯШЁ Ш§ЩҶЪҜШҙШӘШұ ШЁЩҮ ШіЩ…ШӘ ЪҶЩҫ ЩҲ ЫҢШ§ ШұШ§ШіШӘ ШҙШұЩҲШ№ ШЁЩҮ ШҙЩ…ШұШҜЩҶ Щ…ЫҢ Ъ©ЩҶШҜ ШӘШ§ Ш§ЩҶЪҜШҙШӘШұ ШұШ§ ЩҫЫҢШҜШ§ Ъ©ЩҶШҜ (Ш§Щ„ШЁШӘЩҮ ШЁШ§ЫҢШҜ ШЁЩҮ ЩҶШӯЩҲЫҢ ШЁЩҫШұШіШҜ Ъ©ЩҮ Ш·ШұЩҒ ЪҶЩҫ Ш§ЩҲШіШӘ ЫҢШ§ ШұШ§ШіШӘ Ш§ЩҲ Ш§ШіШӘ). Ш§ЪҜШұ ШЁШ§ЩӮЫҢЩ…Ш§ЩҶШҜЩҮ Ш§ШІ ЩҶЩҮ ШЁЫҢШҙШӘШұ ШЁЩҲШҜ ШЁШ§ШІ Ш№ШҜШҜ ЩҶЩҮ ШұШ§ Ш§ШІ ШўЩҶ Ъ©Щ… Ъ©ЩҶШҜ ЩҲ Ш§ЫҢЩҶ Ъ©Ш§Шұ ШұШ§В ШӘШ§ Ш¬Ш§ЫҢЫҢВ Ш§ШҜШ§Щ…ЩҮ ШҜЩҮШҜ Ъ©ЩҮ ШЁШ§ЩӮЫҢЩ…Ш§ЩҶШҜЩҮ Ш§ШІ ЩҶЩҮ Ъ©Щ…ШӘШұ ШЁШ§ШҙШҜ. ШЁЩҮ Ш§ШІШ§ЫҢ ЩҮШұ ШӘЩҒШұЫҢЩӮ Ш§ШІ ЩҶЩҮШҢ ШҙШ№ШЁШҜЩҮ ШЁШ§ШІ Ш№ШҜШҜ ЪҶЩҮШ§Шұ ШұШ§ ШЁЩҮ Ш№ШҜШҜ ШіЩҮ Ъ©ЩҮ ШӘШ§ Ш§ЫҢЩҶШ¬Ш§ ШЁЩҮ ШҜШіШӘ ШўЩҲШұШҜЩҮ ШЁЩҲШҜ ШЁЫҢЩҒШІШ§ЫҢШҜ.
ЫҢЪ© Щ…Ш«Ш§Щ„ Ш№ШҜШҜЫҢ Ш§ЫҢЩҶ Щ…ЩҲШ¶ЩҲШ№ ШұШ§ ШұЩҲШҙЩҶ ШӘШұ Щ…ЫҢ Ъ©ЩҶШҜ. ЩҒШұШ¶ Ъ©ЩҶЫҢШҜ ШўЩҶ ШҙШ®Шө Ш§ЩҶЪҜШҙШӘШұ ШұШ§ ШЁЩҮ ЩҶЩҒШұ ЩҮЩҒШӘЩ… Ш§ШІ ШіЩ…ШӘ ЪҶЩҫ ЩҲ ЫҢШ§ ШұШ§ШіШӘ Ш®ЩҲШҜШҙ ШҜШ§ШҜЩҮ Ш§ШіШӘ. ШЁШ§Шұ Ш§ЩҲЩ„ ЩҶЫҢЩ…ЫҢ Ш§ШІ Ш№ШҜШҜ ЩҮЩҒШӘ ШұШ§ Ъ©ЩҮ ШіЩҮ ЩҲ ЩҶЫҢЩ… Ш§ШіШӘ ШЁЩҮ ШўЩҶ Ш§Ш¶Ш§ЩҒЩҮ Щ…ЫҢ Ъ©ЩҶШҜ ЩҲ ШӯШ§ШөЩ„Шҙ ШҜЩҮ ЩҲ ЩҶЫҢЩ… Щ…ЫҢ ШҙЩҲШҜ. ШөШ§ШӯШЁ Ш§ЩҶЪҜШҙШӘШұ Ш§Ш№Щ„Ш§Щ… Щ…ЫҢ Ъ©ЩҶШҜ Ъ©ЩҮ Ш№ШҜШҜ Ш§Ш№ШҙШ§ШұЫҢ Ш§ШіШӘ. Щ…Ш§ Ш№ШҜШҜ ЫҢЪ© ШұШ§ ЩҶЪҜШ§ЩҮ Щ…ЫҢ ШҜШ§ШұЫҢЩ… . ШіЩҫШі ШЁЩҮ Ш§ЩҲ Щ…ЫҢ ЪҜЩҲЫҢЫҢЩ… ШўЩҶ ШұШ§ ШЁЩҮ ЩҶШІШҜЫҢЪ©ШӘШұЫҢЩҶ Ш№ШҜШҜ Ъ©Ш§Щ…Щ„ Ъ©ЩҶШҜ ЩҲ ШҜЩҲШЁШ§ШұЩҮ ЩҶЫҢЩ…ЫҢ Ш§ШІ ШўЩҶ ШұШ§ ШЁЩҮ ШўЩҶ ШЁЫҢЩҒШІШ§ЫҢШҜ. Ш§ЩҲ ШўЩҶ ШұШ§ ШЁЩҮ ЫҢШ§ШІШҜЩҮ Ъ©Ш§Щ…Щ„ Щ…ЫҢ Ъ©ЩҶШҜ ЩҲ ЩҶЫҢЩ…ЫҢ Ш§ШІ ШўЩҶ ШұШ§ ( Ъ©ЩҮ ЩҫЩҶШ¬ ЩҲ ЩҶЫҢЩ… Ш§ШіШӘ) ШЁЩҮ ШўЩҶ Щ…ЫҢ Ш§ЩҒШІШ§ЫҢШҜ. ШӯШ§ШөЩ„ ШҙШ§ЩҶШІШҜЩҮ ЩҲ ЩҶЫҢЩ… Щ…ЫҢ ШҙЩҲШҜ. ШөШ§ШӯШЁ Ш§ЩҶЪҜШҙШӘШұ Ш§Ш№Щ„Ш§Щ… Щ…ЫҢ ШҜШ§ШұШҜ Ъ©ЩҮ Ш№ШҜШҜ Ш§Ш№ШҙШ§ШұЫҢ Ш§ШіШӘ. Щ…ЫҢ ЪҜЩҲЫҢЫҢЩ… Ъ©ЩҮ ШўЩҶ ШұШ§ Ъ©Ш§Щ…Щ„ Ъ©ЩҶШҜ. Ш§ЩҲ Ш№ШҜШҜ ЩҮЩҒШҜЩҮ ШұШ§ ШЁЩҮ ШҜШіШӘ Щ…ЫҢ ШўЩҲШұШҜ.В Щ…Ш§ Ш№ШҜШҜ ШҜЩҲ ШұШ§ ШЁЩҮ Ш№ШҜШҜ ЫҢЪ© Ъ©ЩҮ ЩҫЫҢШҙ Ш§ШІ Ш§ЫҢЩҶ ЩҶЪҜШ§ЩҮ ШҜШ§ШҙШӘЩҮ Ш§ЫҢЩ… Ш§Ш¶Ш§ЩҒЩҮ Щ…ЫҢ Ъ©ЩҶЫҢЩ…. ШӯШ§Щ„ ШЁЩҮ Ш§ЩҲ Щ…ЫҢ ЪҜЩҲЫҢЫҢЩ… Ш№ШҜШҜ ЩҶЩҮ ШұШ§ Ш§ШІ ШўЩҶ Ъ©Щ… Ъ©ЩҶ. Ш§ЩҲ Ш§ЫҢЩҶ Ъ©Ш§Шұ ШұШ§ Щ…ЫҢ Ъ©ЩҶШҜ ЩҲ ЩҮШҙШӘ ШұШ§ ШЁЩҮ ШҜШіШӘ Щ…ЫҢ ШўЩҲШұШҜ ЩҲ ШҜШұ Ш§ЫҢЩҶ Ш¬Ш§ Щ…ШӘЩҲЩӮЩҒ Щ…ЫҢ ШҙЩҲШҜШҢ ЪҶЩҲЩҶ ШЁЩҮ Ш№ШҜШҜ Ъ©Щ…ШӘШұ Ш§ШІ ЩҶЩҮ ШұШіЫҢШҜЩҮ Ш§ШіШӘ. Щ…Ш§ Ш№ШҜШҜ ЪҶЩҮШ§Шұ ШұШ§ ШЁЩҮ Ш№ШҜШҜ ШіЩҮ Щ…ЫҢ Ш§ЩҒШІШ§ЫҢЫҢЩ… ЩҲ Ш№ШҜШҜ ЩҮЩҒШӘ ШЁЩҮ ШҜШіШӘ Щ…ЫҢ ШўЫҢШҜ. ЩҶШӘЫҢШ¬ЩҮ Щ…ЫҢ ЪҜЫҢШұЫҢЩ… Ъ©ЩҮ ЩҶЩҒШұ ЩҮЩҒШӘЩ… Ш§ЩҶЪҜШҙШӘШұЫҢ ШұШ§ ШҜШұ ШҜШіШӘ ШҜШ§ШұШҜ.
ЩҶЩҲШ№ЫҢ ШҜЫҢЪҜШұ: Ш§ЪҜШұ ЪҜШұЩҲЩҮЫҢ ШҜШұ Щ…Ш¬Щ„ШіЫҢ ШӯШ§Ш¶Шұ ШЁШ§ШҙЩҶШҜШҢ ЫҢЪ©ЫҢ Ш§ШІ Ш§ЫҢШҙШ§ЩҶ Ш№ШҜШҜЫҢ ЪҶЩҶШҜ ЩҫЩҶЩҮШ§ЩҶ Ъ©ШұШҜ ШҜШұ ШҜШіШӘ ЩҲ ЪҜЩҒШӘ Ш§ЫҢЩҶ Ш№ШҜШҜ Ъ©Щ… Ш§ШІ ШҜЩҮ Ш§ШіШӘ Щ…ЫҢвҖҢШ®ЩҲШ§ЩҮЩ… Ъ©ЩҮ Ш§ЩҲ ШұШ§ ШҜЩҮ ЪҜШұШҜШ§ЩҶЫҢ ЩҲ ЫҢЪ©ЫҢ ШҜЫҢЪҜШұ ШІЫҢШ§ШҜШӘ ШЁШҜЩҮЫҢ ЩҲ ЩҮЩ… ЪҶЩҶШҜЫҢЩҶ ШҜЫҢЪҜШұ Ъ©ЩҮ ШҜШ§ШұЩ… ШЁШҜЩҮЫҢ ЩҲ ЩҫЩҶШ¬ Ш§ШІ ШЁЩҮШұ ЩҒЩ„Ш§ЩҶ Ъ©Ші ШЁШҜЩҮЫҢ.В ЩҫШі Щ…Ш§ ШҜЩҮ Ш№ШҜШҜ ШЁШұШҜШ§ШҙШӘЫҢЩ… Ъ©ЩҮ ЩҲШ¬ЩҮ ШҙЩ…Ш§Шұ Ш§ЫҢЩҶ Ш§ШіШӘ. Ш§ШІ ШЁЩҮШұ ШўЩҶ Ъ©ЩҮ ЪҜЩҒШӘ: ШҜЩҮ ЪҜШұШҜШ§ЩҶЫҢ. ЩҲ ЪҜШұ ШЁЫҢШіШӘ ЪҜЩҒШӘЫҢШҢ ШЁЫҢШіШӘ ШЁШұШҜШ§ШҙШӘЫҢЩ…. ЩҲ ШҜЫҢЪҜШұ ЫҢЪ©ЫҢ ШЁШұШҜШ§ШҙШӘЫҢЩ… Ъ©ЩҮ ЫҢЪ©ЫҢ ШІЫҢШ§ШҜШӘ Ш®ЩҲШ§ШіШӘ ЩҲ ЩҫЩҶШ¬ Ш№ШҜШҜ ШҜЫҢЪҜШұ Ш§ШІ ШЁЩҮШұ ШҜЫҢЪҜШұ ЩҒЩ„Ш§ЩҶ ШЁШұШҜШ§ШҙШӘЫҢЩ…. Ш¬Щ…Щ„ЩҮ ШҙШ§ЩҶШІШҜЩҮ ШЁШұШҜШ§ШҙШӘЫҢЩ… ШӘЩ…Ш§Щ…. ЪҜЩҒШӘЩ…: ЩҒШұЩҲ ШұЫҢШІШҢ ЪҶЩҲЩҶ ЩҒШұЩҲ ШұЫҢШ®ШӘШҢ ШҜЩҲ ШЁЩҲШҜ. Щ…Ш§ Ш§ЩҲ ШұШ§ ЩҮШҙШӘ ШЁШұШ§ЩҒШІЩҲШҜЫҢЩ… ШӘШ§ ШҜЩҮ ШҙШҜШҢ ЩҮШҙШӘ Щ…Ш§ ШұШ§ ШЁЩ…Ш§ЩҶШҜШҢ ЫҢЪ©ЫҢ ШҜЫҢЪҜШұ Ш§ЩҲ ШұШ§ ШҜШ§ШҜЫҢЩ… Ш§ШІ ШЁЩҮШұ ШўЩҶ Ъ©ЩҮ ЫҢЪ©ЫҢ ШІЫҢШ§ШҜШӘ Ш®ЩҲШ§ШіШӘЩҮ ШЁЩҲШҜШҢ ЩҮЩҒШӘ ШЁЩ…Ш§ЩҶШҜ. ЩҫЩҶШ¬ ШҜЫҢЪҜШұ Ш§ШІ ШЁШұШ§ЫҢ ЩҒЩ„Ш§ЩҶ ШЁШҜШ§ШҜЫҢЩ…ШҢ ШҜЩҲ ШЁЩ…Ш§ЩҶШҜ. ЪҜЩҒШӘЩ…: Ш§ЫҢЩҶШҢ ШўЩҶ Щ…ЩӮШҜШ§Шұ ШЁЩҲШҜ Ъ©ЩҮ ШӘЩҲ ШҜШ§ШҙШӘЫҢ ЩҲ Ш¬Щ…Щ„ЩҮ ШЁШұ Ш§ЫҢЩҶ Ъ©ШұШҜШ§Шұ ШЁШ§ШҙШҜ.
ШҜШұ Ш§ЫҢЩҶШ¬Ш§ ШҙШ№ШЁШҜЩҮ ШЁШ§ШІ ШЁЩҮ ШҙШ®ШөЫҢ Щ…ЫҢ ЪҜЩҲЫҢШҜ ШЁЩҮ ЫҢЪ© Ш№ШҜШҜ Ъ©Щ…ШӘШұ Ш§ШІ ШҜЩҮ ЩҒЪ©Шұ Ъ©ЩҶШҢ ЩҲ Ш№ШҜШҜЫҢ ШЁЩҮ ШўЩҶ Ш§Ш¶Ш§ЩҒЩҮ Ъ©ЩҶ ШӘШ§ШЁЩҮ ШҜЩҮ ШЁШұШіШҜ. ШіЩҫШі ЫҢЪ© Ш№ШҜШҜ Ш§ШІ Ш№ШҜШҜЫҢ Ъ©ЩҮ ШЁЩҮ ШўЩҶ Ш§ЩҒШІЩҲШҜЫҢ ШӘШ§ ШҜЩҮ ШҙЩҲШҜ Ъ©Щ… Ъ©ЩҶШҢ ЩҫШі Ш§ШІ ШўЩҶ Ш№ШҜШҜ ЩҫЩҶШ¬ ШұШ§ Ш§ШІ ШўЩҶ Ъ©Щ… Ъ©ЩҶ. ШӯШ§Щ„ ШЁЪҜЩҲ ЪҶЩӮШҜШұ ШЁШ§ЩӮЫҢЩ…Ш§ЩҶШҜЩҮ Ш§ШіШӘ. ЩҲЩӮШӘЫҢ Ш§ЩҲ Щ…ЫҢ ЪҜЩҲЫҢШҜ Ш№ШҜШҜ ШҜЩҲ Ш§ШіШӘШҢ Щ…Ш№Щ„ЩҲЩ… Ш§ШіШӘ Ъ©ЩҮ ШЁЩҮ ШҜЩҲ ЩҒЪ©Шұ Ъ©ШұШҜЩҮ Ш§ШіШӘ. ШЁШұШ§ЫҢ Щ…Ш«Ш§Щ„ШҢВ ШӘШөЩҲШұ Ъ©ЩҶЫҢШҜ ШЁЩҮ Ш№ШҜШҜ ШіЩҮ ЩҒЪ©Шұ Ъ©ШұШҜЩҮ Ш§ШіШӘ ЩҲ Ш№ШҜШҜ ЩҮЩҒШӘ ШұШ§ ШЁЩҮ ШўЩҶ Ш§ЩҒШІЩҲШҜЩҮ Ш§ШіШӘ ШӘШ§ ШҜЩҮ ШҙЩҲШҜ. ЩҲЩӮШӘЫҢ Ш§ШІ Ш§ЩҲ Ш®ЩҲШ§ШіШӘЫҢЩ… Ш№ШҜШҜ ШҙШҙ ШұШ§ Ш§ШІ ШўЩҶ Ъ©Щ… Ъ©ЩҶШҜШҢ ЫҢЪ© ШЁШ§ЩӮЫҢ Щ…ЫҢ Щ…Ш§ЩҶШҜ. ЪҶЩҲЩҶ ЩӮШЁЩ„Ш§В ШҙШҙ Ъ©Щ… Ъ©ШұШҜЩҮ ШЁЩҲШҜ ШЁЩҮ Ш§Ш¶Ш§ЩҒЩҮ Ш§ЫҢЩҶ ЫҢЪ© Щ…ЫҢ ШҙЩҲШҜ ЩҮЩҒШӘ. Ш§ЪҜШұ ШўЩҶ ШұШ§ Ш§ШІ ШҜЩҮ Ъ©Щ… Ъ©ЩҶЫҢЩ… Щ…ЫҢ ШҙЩҲШҜ ШіЩҮ.
ЩҶЩҲШ№ЫҢ ШҜЫҢЪҜШұ: ШҜШұ Щ…Ш¬Щ„ШіЫҢ ШӯШ§Ш¶Шұ ШўЫҢЩҶШҜ Ш¬Щ…Ш№ЫҢШҢ ЫҢЪ©ЫҢ Ш§ШІ Ш§ЫҢШҙШ§ЩҶ ЪҜЩҲЫҢШҜ Ъ©ЩҮ: Щ…ЫҢШ§ЩҶ Щ…Ш§ ШҜЩҲ Ъ©Ші ШҜЩҮ Ш№ШҜШҜ ЩҫЩҶЩҮШ§ЩҶ Ш§ШіШӘШҢ ЩҫЫҢШҜШ§ ШЁШ§ЫҢШҜ Ъ©ШұШҜ Ъ©ЩҮ ЩҮШұ Ъ©ЫҢ Ш§ШІ Щ…Ш§ ЪҶЩҶШҜ ШҜШ§ШұШҜ. ЩҲШ¬ЩҮ ШҙЩ…Ш§Шұ ШўЩҶ Ш§ЫҢЩҶ Ш§ШіШӘ Ъ©ЩҮ ШўЩҶ ШҜЩҮ ШұШ§ Ш§ШөЩ„ Ш®ЩҲШ§ЩҶЫҢЩ… ЩҲ ШҜЩҮ ШЁШ§Шұ ШЁШұЩҮЩ… ЪҜЫҢШұЫҢ ШӘШ§ ШөШҜ ШҙЩҲШҜШҢ ЩҲ Ш§ЩҲ ШұШ§ Ш§ШөЩ„ Ш®ЩҲШ§ЩҶЫҢЩ…. ЩҫШі ЪҜЩҲЫҢЫҢЩ…: Ш§ШІ ШўЩҶ ШҜЩҲ ЫҢЪ©ЫҢ ШұШ§ Ъ©ЩҮ ШўЩҶЪҶЩҮ ШӘЩҲ ШҜШ§ШұЫҢШҢ ШҜЩҲ ЪҶЩҶШҜШ§ЩҶ Ъ©ЩҶШҢ ЩҲ ШўЩҶ ШҜЫҢЪҜШұ ШұШ§ ЪҜЩҲЫҢЫҢЩ…: ШўЩҶЪҶЩҮ ШӘЩҲ ШҜШ§ШұЫҢШҢ ШҜЩҮ ЪҶЩҶШҜШ§ЩҶ Ъ©ЩҶ ЩҲ ШўЩҶ Ш¬Щ…Щ„ЩҮ ШЁЩҮ ЩҮЩ… ЪҜШұШҜШўЩҲШұШҢ ЩҲ ШЁЪҜЩҲ Ъ©ЩҮ ЪҶЩҶШҜШіШӘ.В ЪҶЩҲЩҶ ШЁЪҜЩҲЫҢШҜ Ъ©ЩҮ ЪҶЩҶШҜШіШӘ ШӘШ§ Ш§ШІ ШўЩҶ Ш§ШөЩ„ ШЁШұЩҲЫҢЩ…ШҢ ШўЩҶЪҶЩҮ ШЁЩ…Ш§ЩҶШҜ ШЁЩҮ ШҜЩҲ Ъ©Щ…ШӘШұ Ш§ШІ Ш§ШөЩ„ ШЁШЁШ®ШҙЫҢЩ…ШҢ ШўЩҶЪҶЩҮ ШЁШұЩҲШҜШҢ ШҜЩҮШҢ Ш§ШІ Щ…Ш§Щ„ Щ…ШұШҜ ЩҶШ®ШіШӘЫҢЩҶ ШЁШ§ШҙШҜ ЩҲ ШӘЩ…Ш§Щ…ШӘ ШўЩҶ ШҜЩҮШҢ Щ…Ш§Щ„ Щ…ШұШҜ ШҜЩҲЩ… ШЁЩҲШҜ.
Щ…Ш«Ш§Щ„Шҙ: ЪҶЩҶШ§ЩҶ Ъ©ЩҮ Щ…Ш§ ШұШ§ ЪҜЩҒШӘ: ШҜЩҮ Ш№ШҜШҜШіШӘ. Ш§ЫҢЩҶ Ш§ШөЩ„ Ш§ШіШӘШҢ Ш§ЫҢЩҶ Ш§ШөЩ„ ШұШ§ ШҜЩҮ ШЁШ§Шұ ШЁЩҮ ЩҮЩ… ЪҜШұЩҒШӘЫҢЩ…ШҢ ШөШҜ ШЁЩҲШҜ. Ш§ЫҢЩҶ Ш§ШөЩ„ Ш§ШіШӘ. ЩҫШі ЪҜЩҒШӘЫҢЩ… ЫҢЪ©ЫҢ ШұШ§ Ъ©ЩҮ:В Ш§Ш№ШҜШ§ШҜ Ъ©ЩҮ ШӘЩҲ ШҜШ§ШұЫҢ Щ…Ш¶Ш§Ш№ЩҒ Ъ©ЩҶ. ЪҜЩҒШӘ: Ъ©ШұШҜЩ…. ЩҲ ШўЩҶ ШҜЫҢЪҜШұ ШұШ§ ЪҜЩҒШӘЫҢЩ…: ШўЩҶЪҶЩҮ ШӘЩҲ ШҜШ§ШұЫҢ ШҜЩҮ ШЁШ§Шұ ШЁШұЩҮЩ… ЪҜЫҢШұ. ЪҜЩҒШӘ:В ЪҜШұЩҒШӘЩ….В ЪҜЩҒШӘЩ…:В ШЁЪҜЩҲЫҢ Ъ©ЩҮ ЪҶЩҶШҜШіШӘ Ш¬Щ…Щ„ЩҮШҹ ЪҜЩҒШӘ: ЩҮЩҒШӘШ§ШҜЩҲШҙШҙ. ШўЩҶ ШұШ§ Ш§ШІ Ш§ШөЩ„ Ш§ШөЩ„ ШЁШұЩҒШӘЫҢЩ….В ШЁЩ…Ш§ЩҶШҜ ШЁЫҢШіШӘ ЩҲ ЪҶЩҮШ§ШұШҢ ШўЩҶ ШұШ§ ШЁШұ ЩҮШҙШӘ ШЁШ®ШҙЫҢШҜЫҢЩ…ШҢ ШҜЩҲ Ъ©Щ…ШӘШұ Ш§ШІ Ш§ШөЩ„ ШіЩҮ Ш§ШІ ШўЩҶ ШӯШ§ШөЩ„ ШўЩ…ШҜШҢ Щ…Ш№Щ„ЩҲЩ… ШҙШҜ Ъ©ЩҮ ШўЩҶ Щ…ШұШҜ ЩҶШ®ШіШӘЫҢЩҶ ШұШ§ Ъ©ЩҮ ЪҜЩҒШӘЩ… Ъ©ЩҮ Ш№ШҜШҜ ШӘЩҲ ШҜЩҲ ЪҶЩҶШҜШ§ЩҶ Ъ©ЩҶШҢ ШіЩҮ ШҜШ§ШҙШӘШҢ ЩҲ ШӘЩ…Ш§Щ…ШӘ ШіЩҮ ШӘШ§ ШҜЩҮШҢ ЩҮЩҒШӘ ШЁШ§ШҙШҜ. Ш§ЫҢЩҶ Щ…ШұШҜ ШҜЫҢЪҜШұ ШҜШ§ШҙШӘ Ъ©ЩҮ Ш§ЩҲ ШұШ§ ЪҜЩҒШӘЫҢЩ… ШўЩҶЪҶЩҮ ШӘЩҲ ШҜШ§ШұЫҢ ШҜЩҮ ШЁШ§Шұ ШЁШұЩҮЩ… ЪҜЫҢШұ ШӘШ§ Щ…Ш№Щ„ЩҲЩ… ШҙШҜ Ъ©ЩҮ Ш§ЩҲ ЩҮЩҒШӘ ШҜШ§ШұШҜ.
ШҜШұ Ш§ЫҢЩҶШ¬Ш§ ШЁЩҮ ШЁЩҮ ШҜЩҲ ЩҶЩҒШұ Щ…ЫҢ ЪҜЩҲЫҢЫҢЩ… Ъ©ЩҮ ШҜЩҲ Ш№ШҜШҜ ШұШ§ Ш§ЩҶШӘШ®Ш§ШЁ Ъ©ЩҶЫҢШҜ Ъ©ЩҮ Щ…Ш¬Щ…ЩҲШ№ ШўЩҶ ШҜЩҮ ШҙЩҲШҜ. ЫҢЪ©ЫҢ Ш№ШҜШҜ ШіЩҮ ШұШ§ Ш§ЩҶШӘШ®Ш§ШЁ Щ…ЫҢ Ъ©ЩҶШҜ ЩҲШҜЫҢЪҜШұЫҢ Ш№ШҜШҜ ЩҮЩҒШӘ ШұШ§. ШЁЩҮ Ш§ЩҲЩ„ЫҢ Щ…ЫҢ ЪҜЩҲЫҢЫҢЩ… Ш№ШҜШҜЫҢ ШұШ§ Ъ©ЩҮ Ш§ЩҶШӘШ®Ш§ШЁ Ъ©ШұШҜЩҮ Ш§ЫҢ Ш¶ШұШЁШҜШұ ШҜЩҲ Ъ©ЩҶ ЩҲ ШЁЩҮ ЩҶЩҒШұ ШҜЩҲЩ…ЫҢ Щ…ЫҢ ЪҜЩҲЫҢЫҢЩ… Ъ©ЩҮ ШўЩҶ ШұШ§ Ш¶ШұШЁ ШҜШұ ШҜЩҮ Ъ©ЩҶШҜ ЩҲ ШӯШ§ШөЩ„ ЩҮШұШҜЩҲ Ш№ШҜШҜ ШұШ§ ШЁШ§ ЩҮЩ… Ш¬Щ…Ш№ Ъ©ЩҶЩҶШҜ ЩҲ ШЁЩҮ Щ…Ш§ ШЁЪҜЩҲЫҢЩҶШҜ. ШЁЩҮ Щ…Ш§ Щ…ЫҢ ЪҜЩҲЫҢЩҶШҜ Ъ©ЩҮ ШӯШ§ШөЩ„ ШҜЩҲ Ш№ШҜШҜ ЩҮЩҒШӘШ§ШҜ ЩҲШҙШҙ Щ…ЫҢ ШҙЩҲШҜ. Щ…Ш§ Ш№ШҜШҜ ШҜЩҮ ШұШ§ Ш¶ШұШЁШҜШұ ШҜЩҮ Щ…ЫҢ Ъ©ЩҶЫҢЩ… ШӘШ§ ШөШҜ ШҙЩҲШҜШҢ ШіЩҫШі ЩҮЩҒШӘШ§ШҜ ЩҲ ШҙШҙ ШұШ§ Ш§ШІ ШөШҜ Ъ©Щ… Щ…ЫҢ Ъ©ЩҶЫҢЩ… ШӘШ§ Ш№ШҜШҜ ШЁЫҢШіШӘ ЩҲ ЪҶЩҮШ§Шұ ШЁЩҮ ШҜШіШӘ ШўЫҢШҜ. ШўЩҶ ШұШ§ ШЁШұ ЩҮШҙШӘ ШӘЩӮШіЫҢЩ… Щ…ЫҢ Ъ©ЩҶЫҢЩ… ШӘШ§ Ш№ШҜШҜ ШіЩҮ ШЁЩҮ ШҜШіШӘ ШўЫҢШҜ. Ш§ЫҢЩҶ Ш№ШҜШҜЫҢ Ш§ШіШӘ Ъ©ЩҮ ЩҶЩҒШұ Ш§ЩҲЩ„ ШЁЩҮ ШўЩҶ ЩҒЪ©Шұ Ъ©ШұШҜЩҮ Ш§ШіШӘ. ШўЩҶ ШұШ§ Ш§ШІ ШҜЩҮ Ъ©Щ… Щ…ЫҢ Ъ©ЩҶЫҢЩ… Ш№ШҜШҜ ЩҮЩҒШӘ ШЁЩҮ ШҜШіШӘ Щ…ЫҢ ШўЫҢШҜ Ъ©ЩҮ ЩҶЩҒШұ ШҜЩҲЩ… ШЁЩҮ ШўЩҶ ЩҒЪ©Шұ Ъ©ШұШҜЩҮ Ш§ШіШӘ.
Ш§ЫҢЩҶ ЫҢЪ© ШҜШіШӘЪҜШ§ЩҮ ШҜЩҲ Щ…Ш№Ш§ШҜЩ„ЩҮ ШҜЩҲ Щ…Ш¬ЩҮЩҲЩ„ЫҢ Ш§ШіШӘ Ъ©ЩҮ Ш§ШІ Ш·ШұЫҢЩӮ Ш¬ШЁШұЫҢ ЩҮЩ… Щ…ЫҢ ШҙЩҲШҜ ШўЩҶ ШұШ§ ШЁЩҮ Ш§ЫҢЩҶ ШӘШұШӘЫҢШЁ ШӯЩ„ Ъ©ШұШҜ: (P ШӯШ§ШөЩ„ Ш¬Щ…Ш№ ШҜЩҲ Ш№ШҜШҜ ЩҫШі Ш§ШІ ШҜЩҲ ШЁШұШ§ШЁШұ ЩҲ ШҜЩҮ ШЁШұШ§ШЁШұ Ъ©ШұШҜЩҶ ШўЩҶЩҮШ§ Ш§ШіШӘ)::
В x+y=10 Гһ y=10-x
В 2x+10y=P Гһ 2x+10(10-x)=P Гһ 2x+100-10x=P Гһ 8x=100-P Гһ x=(100-P)/8
Ш§ЪҜШұ ШҜШұ Щ…ЫҢШ§ЩҶ ЪҜШұЩҲЩҮЫҢ ШіЩҮ Ъ©Ші ЪҜЩҲЫҢШҜ Ъ©ЩҮ: Щ…Ш§ ШіЩҮ Ъ©Ші ШҜЩҲШ§ШІШҜЩҮ Ш№ШҜШҜ ШҜШ§ШұЫҢЩ…ШҢ ЩҫЫҢШҜШ§ ШЁШ§ЫҢШҜ Ъ©ШұШҜ Ъ©ЩҮ ЩҮШұ ЫҢЪ©ЫҢ ЪҶЩҶШҜ ШҜШ§ШұЫҢЩ…Шҹ Ъ©ЩҮ ШҜЩҲШ§ШІШҜЩҮ ШұШ§ Ш§ШөЩ„ Ш®ЩҲШ§ЩҶЫҢЩ…. ЩҲ ШўЩҶЪҜЩҮ ШҜЩҲШ§ШІШҜЩҮ (ШұШ§) ШҜЩҲШ§ШІШҜЩҮ ШЁШ§Шұ ШЁШұ ЩҮЩ… ЪҜЫҢШұЫҢЩ… ШӘШ§ ШөШҜЩҲ ЪҶЩҮЩ„ ЩҲ ЪҶЩҮШ§Шұ ШӯШ§ШөЩ„ ШҙЩҲШҜ. Ш§ЫҢЩҶ ШұШ§ Ш§ШөЩ„ Ш§ШөЩ„ Ш®ЩҲШ§ЩҶЫҢЩ… ЩҲ ЩҶЪҜШ§ЩҮ ШҜШ§ШұЫҢЩ… ЩҲ ЫҢЪ©ЫҢ ШұШ§ ЪҜЩҲЫҢЫҢЩ…:В ШўЩҶЪҶЩҮ ШӘЩҲ ШҜШ§ШұЫҢ ШҜЩҲЪҶЩҶШҜШ§ЩҶ Ъ©ЩҶ ЩҲ ШҜЫҢЪҜШұЫҢ ШұШ§ ЪҜЩҲЫҢЫҢЩ…: ШўЩҶЪҶЩҮ ШӘЩҲ ШҜШ§ШұЫҢ ЫҢШ§ШІШҜЩҮ ШЁШ§Шұ ШЁШұЩҮЩ… ЪҜЫҢШұ ЫҢЪ©ЫҢ Ъ©Щ…ШӘШұ Ш§ШІ Ш§ШөЩ„ ЩҲ ШўЩҶ ШіЫҢЩ… ШұШ§ ЪҜЩҲЫҢЫҢЩ…: ШўЩҶЪҶЩҮ ШӘЩҲ ШҜШ§ШұЫҢ ШҜЩҲШ§ШІШҜЩҮ ШЁШ§Шұ ШЁШұЩҮЩ… ЪҜЫҢШұ. ЪҶЩҲЩҶ Ъ©ШұШҜЩҶШҜШҢ ШЁЩҫШұШіЫҢЩ… Ъ©ЩҮ: Ш¬Щ…Щ„ЩҮ ЪҶЩҶШҜШіШӘШҹ ЪҶЩҲЩҶ ЪҜЩҒШӘШҢ Щ…Ш§ Ш№ШҜШҜ Ш§ШІ Ш§ШөЩ„ Ш§ШөЩ„ ШЁШұЩҲЫҢЩ….В ШЁШ§ЩӮЫҢ ШұШ§ Ъ©ЩҮ ШЁЩ…Ш§ЩҶШҜ ШЁШұ ШҜЩҮ Ъ©ЩҮ ШҜЩҲ Ъ©Щ…ШӘШұ Ш§ШІ Ш§ШөЩ„ Ш§ШіШӘШҢ ШЁШЁШ®ШҙЫҢЩ…. ШўЩҶЪҶЩҮ ШЁШұЩҲШҜШҢ Ш№ШҜШҜ Щ…ШұШҜ ЩҶШ®ШіШӘЫҢЩҶ ШЁШ§ШҙШҜ Ъ©ЩҮ Ш№ШҜШҜ ЩҲЫҢ ШҜЩҲ ЪҶЩҶШҜШ§ЩҶ Ъ©ШұШҜЩҮ ШЁЩҲШҜЫҢЩ…ШҢ ЩҲ ШӘЩ…Ш§Щ…ШӘ ЩҮШұ ШҜЩҲ ШЁЩҮ Ш§ШөЩ„ Щ…ШұШҜ ШіЫҢЩ… ШЁШ§ШҙШҜ.
Щ…Ш«Ш§Щ„Шҙ: ЪҶЩҶШ§ЩҶ Ъ©ЩҮ Щ…ЫҢШ§ЩҶ ШіЩҮ Ъ©Ші ШіЩҮ Ш№ШҜШҜ ЩҫЩҶЩҮШ§ЩҶ Ъ©ШұШҜЩҶШҜ Ъ©ЩҮ Ш¬Щ…Щ„ЩҮ ШҜЩҲШ§ШІШҜЩҮ ШЁШ§ШҙШҜШҢ ЩҲ Ш§ЫҢЩҶ ШҜЩҲШ§ШІШҜЩҮ Ш§ШөЩ„ Ш§ШіШӘ. ЩҫШі Ш§ЫҢЩҶ ШҜЩҲШ§ШІШҜЩҮ ШұШ§ ШҜЩҲШ§ШІШҜЩҮ ШЁШ§Шұ ШЁШұЩҮЩ… ЪҜШұЩҒШӘЫҢЩ…ШҢ ШөШҜЩҲЪҶЩҮЩ„ ЩҲ ЪҶЩҮШ§Шұ ШҙШҜШҢ Ш§ЫҢЩҶ Ш¬Щ…Щ„ЩҮ Ш§ШөЩ„ Ш§ШөЩ„ Ш§ШіШӘ.В ЩҫШі ЫҢЪ©ЫҢ ШұШ§ ЪҜЩҒШӘЫҢЩ…:В ШўЩҶЪҶЩҮ ШӘЩҲ ШҜШ§ШұЫҢ Щ…Ш¶Ш§Ш№ЩҒ Ъ©ЩҶШҢ ЩҲ ШҜЫҢЪҜШұЫҢ ШұШ§ ЪҜЩҒШӘЫҢЩ…:В ШўЩҶЪҶЩҮ ШӘЩҲ ШҜШ§ШұЫҢ ЫҢШ§ШІШҜЩҮ ШЁШ§ШұШЁШұ ЩҮЩ… ЪҜЫҢШұ ЫҢЪ©ЫҢ Ъ©Щ…ШӘШұ Ш§ШІ Ш§ШөЩ„ШҢ ЩҲ ШіЫҢЩ… ШұШ§ ЪҜЩҒШӘЫҢЩ…: ШўЩҶЪҶЩҮ ШӘЩҲ ШҜШ§ШұЫҢ ШҜЩҲШ§ШІШҜЩҮ ШЁШ§Шұ ШЁШұЩҮЩ… ЪҜЫҢШұ ЪҶЩҶШҜШ§ЩҶ Ъ©ЩҮ Ш§ШөЩ„ Ш§ШіШӘ. ЪҶЩҲЩҶ Ъ©ШұШҜЩҶШҜШҢ ШЁЩҫШұШіЫҢЩ… Ъ©ЩҮ Ш¬Щ…Щ„ЩҮ ЪҶЩҶШҜШіШӘШҹ ЪҜЩҒШӘ:В ШөШҜЩҲШЁЫҢШіШӘ. Ш§ШІ Ш№ШҜШҜ ШўЩҶ ШөШҜ ЩҲ ЪҶЩҮЩ„ ЩҲ ЪҶЩҮШ§Шұ ШЁШұЩҒШӘЫҢЩ… ШЁЩ…Ш§ЩҶШҜ ШЁЫҢШіШӘ ЩҲ ЪҶЩҮШ§ШұЪ©ЩҮВ Ш§ЩҲ ШұШ§ ШЁШұ ШҜЩҮ ШЁШ®ШҙЫҢШҜЫҢЩ… Ъ©ЩҮ ШҜЩҲ Ъ©Щ…ШӘШұ Ш§ШІ Ш§ШөЩ„ Ш§ШіШӘ. ШЁШұЩҒШӘШҢ ШҜЩҲ ШЁЩ…Ш§ЩҶШҜШҢ ЪҶЩҮШ§Шұ. ЪҜЩҒШӘЫҢЩ… Ъ©ЩҮ: Ш№ШҜШҜ Щ…ШұШҜ ЩҶШ®ШіШӘЫҢЩҶ Ш§ШіШӘ Ъ©ЩҮ Ш№ШҜШҜ Ш§ЩҲ ШҜЩҲ ЪҶЩҶШҜШ§ЩҶ Ъ©ШұШҜЩҮ ШЁЩҲШҜЫҢЩ…. ЩҲ ЪҶЩҮШ§Шұ Ъ©ЩҮ ШЁЩ…Ш§ЩҶШҜШҢ Ш№ШҜШҜ ШўЩҶ Щ…ШұШҜШіШӘ Ъ©ЩҮ Ш§ЩҲ ШұШ§ ЫҢШ§ШІШҜЩҮ ЫҢШ§ШІШҜЩҮ ШЁШұЩҮЩ… ЪҜШұЩҒШӘЩҮ ШЁЩҲШҜЫҢЩ…. ЪҶЩҮШ§Шұ ЩҲ ШҜЩҲ ШӘШ§ ШҜЩҲШ§ШІШҜЩҮШҢ ШҙШҙ ШЁШ§ШҙШҜШҢ ШўЩҶ Щ…ШұШҜ ШіЫҢЩ… Ш§ШіШӘ Ъ©ЩҮ ШҜЩҲШ§ШІШҜЩҮ ШЁШ§Шұ ШҜЩҲШ§ШІШҜЩҮ ШЁШұЩҮЩ… ЪҜШұЩҒШӘЩҮ ШЁЩҲШҜЫҢЩ….
Ш§ШҜШұ Ш§ЫҢЩҶ Щ…ШіШҰЩ„ЩҮ ШіЩҮ ЩҶЩҒШұ ШЁЩҮ ШіЩҮ Ш№ШҜШҜ ЩҒЪ©Шұ Щ…ЫҢ Ъ©ЩҶЩҶШҜ Ъ©ЩҮ Щ…Ш¬Щ…ЩҲШ№ ШўЩҶЩҮШ§ ШҜЩҲШ§ШІШҜЩҮ Щ…ЫҢ ШҙЩҲШҜ. ШЁЩҮ ЩҶЩҒШұ Ш§ЩҲЩ„ Щ…ЫҢ ЪҜЩҲЫҢЫҢЩ… Ш№ШҜШҜ Ш®ЩҲШҜ ШұШ§ Ш¶ШұШЁШҜШұ ШҜЩҲ Ъ©ЩҶШҜШҢ ШЁЩҮ ЩҶЩҒШұ ШҜЩҲЩ… Щ…ЫҢ ЪҜЩҲЫҢЫҢЩ… Ш№ШҜШҜШҙ ШұШ§ Ш¶ШұШЁШҜШұ ЫҢШ§ШІШҜЩҮ Ъ©ЩҶШҜ ЩҲ ШЁЩҮ ЩҶЩҒШұ ШіЩҲЩ… Щ…ЫҢ ЪҜЩҲЫҢЫҢЩ… ШўЩҶ ШұШ§ Ш¶ШұШЁШҜШұ ШҜЩҲШ§ШІШҜЩҮ Ъ©ЩҶШҜ ЩҲ Ш¬Щ…Ш№ Ш§ЫҢЩҶ ШӯШ§ШөЩ„ Ш¶ШұШЁ ЩҮШ§ ШұШ§ ШЁЩҮ Щ…Ш§ ШЁЪҜЩҲЫҢШҜ. Ш№ШҜШҜ ШӯШ§ШөЩ„ ШұШ§ Ш§ШІ ШөШҜ ЩҲ ЪҶЩҮЩ„ ЩҲ ЪҶЩҮШ§Шұ (ШӯШ§ШөЩ„ Ш¶ШұШЁ ШҜЩҲШ§ШІШҜЩҮ ШҜШұ ШҜЩҲШ§ШІШҜЩҮ) Ъ©Щ… Щ…ЫҢ Ъ©ЩҶЫҢЩ…. ЩҒШұШ¶ Ъ©ЩҶЫҢШҜ ЪҜЩҒШӘЩҮ Ш§ЩҶШҜ ШөШҜ ЩҲ ШЁЫҢШіШӘ. ШЁЩҶШ§ШЁШұШ§ЫҢЩҶ ШЁШ§ЩӮЫҢЩ…Ш§ЩҶШҜЩҮ Щ…ЫҢ ШҙЩҲШҜ ШЁЫҢШіШӘ ЩҲ ЪҶЩҮШ§Шұ. ШўЩҶ ШұШ§ ШЁЩҮ ШҜЩҮ ШӘЩӮШіЫҢЩ… Щ…ЫҢ Ъ©ЩҶЫҢЩ…ШҢ Щ…ЫҢ ШҙЩҲШҜ ШҜЩҲ. ШЁШ§ЩӮЫҢЩ…Ш§ЩҶШҜЩҮ Ш№ШҜШҜ ЪҶЩҮШ§Шұ Ш§ШіШӘ. ШҜЩҲ Ш№ШҜШҜ Щ…ШұШҜ Ш§ЩҲЩ„ЫҢ Ш§ШіШӘ Ъ©ЩҮ ШўЩҶ ШұШ§ Ш¶ШұШЁШҜШұ ШҜЩҲ Ъ©ШұШҜЩҮ ШЁЩҲШҜ ЩҲ ЪҶЩҮШ§Шұ Ш№ШҜШҜ Щ…ШұШҜ ШҜЩҲЩ…ЫҢ Ш§ШіШӘ Ъ©ЩҮ Ш¶ШұШЁШҜШұ ЫҢШ§ШІШҜЩҮ Ъ©ШұШҜЩҮ ШЁЩҲШҜ. Ш¬Щ…Ш№ ЪҶЩҮШ§Шұ ЩҲ ШҜЩҲ Щ…ЫҢ ШҙЩҲШҜ ШҙШҙ Ъ©ЩҮ Ш§ЪҜШұ Ш§ШІ ШҜЩҲШ§ШІШҜЩҮ Ъ©Щ… Ъ©ЩҶЫҢЩ… Ш№ШҜШҜ ШҙШҙ Щ…ЫҢ Щ…Ш§ЩҶШҜ Ъ©ЩҮ Ш№ШҜШҜ ЩҶЩҒШұ ШіЩҲЩ… Ш§ШіШӘ Ъ©ЩҮ Ш¶ШұШЁШҜШұ ШҜЩҲШ§ШІШҜЩҮ Ъ©ШұШҜЩҮ ШЁЩҲШҜ.
ЩҶЩҲШ№ЫҢ ШҜЫҢЪҜШұ:В ЩҮЩ…ЫҢЩҶ ШҙЩ…Ш§Шұ ШҜШұ Щ…ЫҢШ§ЩҶ Ш¬Щ…Ш№ЫҢ ШЁШӘЩҲШ§ЩҶ Ъ©ШұШҜЩҶ ЩҲ ЩҶЫҢЪ©ЩҲ ШЁШ§ШҙШҜ:В ШЁШ§ЫҢШҜ Ъ©ЩҮ Щ…ШҙШӘЫҢ ЩҶШ®ЩҲШҜ ШЁЫҢШ§ЩҲШұЩҶШҜ ЩҲ ШҜЩҮ ШҜШ§ЩҶЩҮ Ш§ШІ ШўЩҶ Ш¬Щ…Щ„ЩҮ ШЁШұШҜШ§ШұЩҶШҜ ЩҲ ШіЩҮ Ъ©Ші ШұШ§ ШҜЩҮЩҶШҜ ШӘШ§ ЩҮШұ Ъ©Ші ЪҶЩҶШҜШ§ЩҶ Ъ©ЩҮ Ш®ЩҲШ§ЩҮШҜШҢ ЩҫЩҶЩҮШ§ЩҶ Ъ©ЩҶШҜ. ЪҶЩҲЩҶ Ъ©ШұШҜЩҶШҜШҢ ШөШҜ ШҜШ§ЩҶЩҮ ШҜЫҢЪҜШұ ШЁШұ Ш·ШЁЩӮЫҢ Ъ©ЩҶЩҶШҜ. Ш§ЪҜШұ ШўЩҶ Ъ©ЩҮ ШҜШ§ШҜЩҮ ШЁЩҲШҜЩҶШҜШҢ ШҜЩҮ ШҜШ§ЩҶЩҮ ШЁЩҲШҜШҢ ШІЫҢШұШ§ ШЁШ§ЫҢШҜ ШҜЩҮ ЪҶЩҶШҜШ§ЩҶ ШӘЩҲ ШЁЩҲШҜШҢ ЩҲ (ЩҫШі ШЁЩҮ ШҙШ®Шө Ш§ЩҲЩ„ ШЁЪҜЩҲ) ШҜЩҲ ЪҶЩҶШҜШ§ЩҶ Ъ©ЩҮ ШӘЩҲ ШҜШ§ШұЫҢ ШЁШұШҜШ§Шұ ЩҫЩҶЩҮШ§ЩҶШҢ ЩҲ ЪҶЩҮШ§Шұ Ъ©ШіЫҢ ШұШ§ ШҜЩҮ. ЪҶЩҲЩҶ (ЩҶШ®ЩҲШҜЩҮШ§ ШұШ§ ШЁЩҮ ШўЩҶ ШҙШ®Шө) ШҜШ§ШҜ. (ШЁЩҮ ШҙШ®Шө) ШҜЩҲЩ…В (ШЁЪҜЩҲ) ЩҶЩҮ ЪҶЩҶШҜШ§ЩҶ Ъ©ЩҮ ШӘЩҲ ШҜШ§ШұЫҢ ШЁШұШҜШ§ШұШҜ (ШҜШұ Ш§ЫҢЩҶШ¬Ш§ ЪҶЩҶШҜ Ъ©Щ„Щ…ЩҮ Ш¬Ш§ Ш§ЩҒШӘШ§ШҜЩҮВ Ъ©ЩҮ ШЁШ§ЫҢШҜ Ш§ЫҢЩҶ ШЁШ§ШҙШҜ: ШЁЩҮ ЩҫЩҶШ¬Щ… Ъ©Ші ШҜЩҮ. ЩҲЩӮШӘЫҢ ЪҶЩҶЫҢЩҶ Ъ©ШұШҜ ШЁЩҮ ШіЩҲЩ… Ъ©Ші ШЁЪҜЩҲ ШҜЩҮ ЪҶЩҶШҜШ§ЩҶ Ъ©ЩҮ ШӘЩҲ ШҜШ§ШұЫҢ) ШҙШҙЩ… Ъ©ШіЫҢ ШұШ§ ШҜЩҮ.В ЪҶЩҲЩҶ Ъ©ШұШҜЩҶШҜ ЩҲ ШҜШ§ШҜЩҶШҜШҢ ШўЩҶ ШЁШ§ЩӮЫҢ ШұШ§ Ъ©ЩҮ ШЁШұ Ш·ШЁЩӮ ШЁШ§ШҙШҜШҢ ЩҮШұ ЩҮШҙШӘЫҢ Ъ©ЩҮ Ш§ЩҶШҜШұ ЩҲЫҢ ШЁШ§ШҙШҜШҢ ШЁЫҢЩҒЪҜЩҶШҢ ЩҲ ЩҶЪҜШ§ЩҮ ШҜШ§Шұ Ъ©ЩҮ ЪҶЩҶШҜ Ш§ЩҒЪҜЩҶШҜЩҶШҜ Ъ©ЩҮ ШўЩҶ Ш№ШҜШҜ Щ…ШұШҜ ЩҶШ®ШіШӘЫҢЩҶ ШЁШ§ШҙШҜ Ъ©ЩҮ ШҜЩҲ ЪҶЩҶШҜШ§ЩҶ (ЩҶШ®ЩҲШҜ) ШЁЩҮ Щ…ШұШҜЩ… ЪҶЩҮШ§ШұЩ… ШҜШ§ШҜ. ЩҫШі ЪҶЩҮШ§ШұЩ… ШұШ§ ЪҜЩҲЫҢЩҶШҜ Ъ©ЩҮ ШӘЩҲ ШҜЩҲЪҶЩҶШҜШ§ЩҶ ШҜШ§ШұЫҢШҢ ЩҲ ШўЩҶЪҶЩҮ ШЁШұ Ш·ШЁЩӮ ШЁЩ…Ш§ЩҶШҜШҢ ШўЩҶ ЩҮШҙШӘШҢ Ш№ШҜШҜ Щ…ШұШҜ ШҜЩҲЩ… ШЁЩҲШҜШҢ ЩҲ ЩҫЩҶШ¬Щ… ЩҫШ§ЩҶШІШҜЩҮ ШЁШ§Шұ (ШЁШ§ЫҢШҜ ЩҶЩҮ ШЁШ§Шұ ШЁШ§ШҙШҜ) ЪҶЩҶШҜШ§ЩҶ ШҜШ§ШұШҜ ЩҲ ШӘЩ…Ш§Щ…ШӘ (Щ…Ш¬Щ…ЩҲШ№ Ш№ШҜШҜ) Щ…ШұШҜ ЩҶШ®ШіШӘЫҢЩҶ ЩҲ ШҜЩҲЩ… ШӘШ§ ШҜЩҮШҢ Ш№ШҜШҜ ШўЩҶ Щ…ШұШҜ ШіЫҢЩ… ШЁШ§ШҙШҜ ЩҲ ШҜЩҮ ЪҶЩҶШҜШ§ЩҶ Щ…ШұШҜ ШҙШҙЩ… ШҜШ§ШҜШҢ ЩҲ Ш¬Щ…Щ„ЩҮ ШЁШұ Ш§ЫҢЩҶ Ъ©ШұШҜШ§Шұ ШЁШ§ШҙШҜ.
Щ…ШіШҰЩ„ЩҮ ШЁШ§Щ„Ш§ЫҢЫҢ ЩҒШұЩӮ ШӘШөШӯЫҢШӯ Ш§ШҜШЁЫҢ ЩҲ Ш№Щ„Щ…ЫҢ ШұШ§ ШЁЩҮ Ш®ЩҲШЁЫҢ ЩҶШҙШ§ЩҶ Щ…ЫҢ ШҜЩҮШҜ. Ш§ЫҢЩҶ Щ…ШіШҰЩ„ЩҮ ЫҢЪ© Ш¬Ш§Ш§ЩҒШӘШ§ШҜЪҜЫҢ ШҜШ§ШұШҜ ЩҲ ШўЩҶ ЩҶЩҒШұ ШіЩҲЩ… Ш§ШіШӘ Ъ©ЩҮ Щ…Ш№Щ„ЩҲЩ… ЩҶЫҢШіШӘ ЪҶЩҶШҜ ШЁШұШ§ШЁШұ ЩҶШ®ЩҲШҜ ШЁЩҮ Щ…ШұШҜ ЩҫЩҶШ¬Щ… ШҜШ§ШҜЩҮ Ш§ШіШӘ. ЩҮЩ… ЪҶЩҶЫҢЩҶ ЫҢЪ© Ш¬Щ…Щ„ЩҮ ШӘЪ©ШұШ§ШұЫҢ Ъ©ЩҮ Щ…Ш§ ШўЩҶ ШұШ§ ШҜШұ ЩҫШұШ§ЩҶШӘШІ ЪҜШ°Ш§ШҙШӘЩҮ Ш§ЫҢЩ…. ШӯЩ„ Ш§ЫҢЩҶ Щ…ШіШҰЩ„ЩҮ ШЁЩҮ Ш§ЫҢЩҶ ШҙЪ©Щ„ Ш§Щ…Ъ©Ш§ЩҶ ЩҶШҜШ§ШұШҜШҢ ЪҶЩҲЩҶ Ш§Ш·Щ„Ш§Ш№Ш§ШӘ Щ„Ш§ШІЩ… ШЁШұШ§ЫҢ Щ…ШӯШ§ШіШЁЩҮ Ш¬Ш§ Ш§ЩҒШӘШ§ШҜЩҮ Ш§ШіШӘ.
Ш§ЪҜШұ Ш¬Щ…Ш§Ш№ШӘЫҢ ШӯШ§Ш¶Шұ ШўЫҢЩҶШҜ ЩҲ ЪҜЩҲЫҢЩҶШҜ ШіЩҮ ЩҫШ§ШұЩҮ ЩӮЩ„Щ… ЫҢШ§ ЪҶЩҲШЁ ШұШ§ ШЁЩҮ ШіЩҮ ШІШ®Щ… ЪҶЩҲЩҶ ШЁШІЩҶЫҢЩ…ШҢ ЩҶЩҮ ЩҫШ§ШұЩҮ ШӯШ§ШөЩ„ ШўЫҢШҜШҹ ЪҶЩҲЩҶ ЪҶЩҶЫҢЩҶ Ш®ЩҲШ§ЩҮЫҢЩ…ШҢ ЩҲШ¬ЩҮ ШЁШұЫҢШҜЩҶ ШўЩҶ ШЁШ§ШҙШҜ Ъ©ЩҮ ЩҮШұ ШіЩҮ ЪҶЩҲШЁ ШұШ§ Щ…Ш«Щ„Ш«ЫҢ ШіШ§ШІЫҢЩ… ЪҶЩҶШ§ЩҶ Ъ©ЩҮ ШҜШұ ШўЩҶ Щ…Ш«Щ„Ш« ШіЩҮ Ш№ЩӮШҜ ШӯШ§ШөЩ„ ШўЫҢШҜ. ЩҫШі ШЁЩҮ ЩҮШұ Ш№ЩӮШҜЫҢ ШІШ®Щ… ШІЩҶЫҢЩ…ШҢ ЩҶЩҮ ЩҫШ§ШұЩҮ ЪҜШұШҜШҜ ШЁШұ Ш§ЫҢЩҶ Ъ©ШұШҜШ§Шұ :
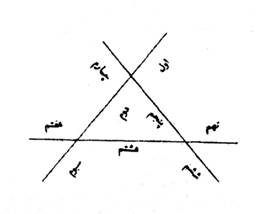
Ш§ЫҢЩҶ ЫҢЪ© Щ…ШіШҰЩ„ЩҮ ЩҮЩҶШҜШіЫҢ Ш§ШіШӘ. ШіЩҮ Ш®Ш· ШұШ§ ШҜШұ ШіЩҮ ЩҶЩӮШ·ЩҮ Ш·ЩҲШұЫҢ ШЁШ§ ЩҮЩ…ШҜЫҢЪҜШұ ЩӮШ·Ш№ Ъ©ЩҶЫҢШҜ Ъ©ЩҮ ЩҶЩҮ ЩӮШ·Ш№ЩҮ ШҙЩҲШҜ. ШҜШұ ШҙЪ©Щ„ ШЁШ§Щ„Ш§ ЩӮШ·Ш№Ш§ШӘ Щ…ШҙШ®Шө ШҙШҜЩҮ Ш§ЩҶШҜ.
ШҜЫҢЪҜШұ Ш§ЪҜШұ ЪҜЩҲЫҢЩҶШҜ Ъ©ЩҮ Ш®ЩҲШ§ЩҮЫҢЩ… Ъ©ЩҮ ШіЩҮ ЩҫШ§ШұЩҮ ЪҶЩҲШЁ ШұШ§ ШЁЩҮ ШҜЩҲ ШІШ®Щ… ШЁЩҮ ЩҮЩҒШӘ ЩҫШ§ШұЩҮ Ъ©ЩҶЫҢЩ…ШҢ ЪҶЩҲЩҶ ШЁШ§ЫҢШҜ Ъ©ШұШҜЩҶШҹ ШЁШ§ЫҢШҜ Ъ©ЩҮ ШҜЩҲ ЪҶЩҲШЁ ШЁЩҶЩҮЩҶШҜ ЩҲ ШЁШұ ШЁШ§Щ„Ш§ЫҢ ЩҮШұ ШҜЩҲ ЫҢЪ©ЫҢ ШЁШұ ЩҫЩҮЩҶШ§ ШЁШұ Ш§ЫҢЩҶ Ъ©ШұШҜШ§Шұ Ъ©ЩҮ ЩҶЩ…ЩҲШҜЫҢЩ… ШӘШ§ ШҜЩҲ Ш№ЩӮШҜ ШӘЩӮШ§Ш·Ш№ ШЁШұ ЩҲЫҢ ЩҫШҜЫҢШҜ ШўЫҢШҜ. ЩҫШі ЩҮШұ Ш№ЩӮШҜЫҢ ШІШ®Щ… ШЁШІЩҶЩҶШҜШҢ ЩҮЩҒШӘ ЩҫШ§ШұЩҮ ЪҜШұШҜШҜ ЪҶЩҶЫҢЩҶ Ъ©ЩҮ ЩҫЫҢШҜШ§ Ъ©ШұШҜЫҢЩ…:
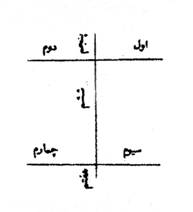
ШҜШұ Ш§ЫҢЩҶ Щ…ШіШҰЩ„ЩҮ ЩҮЩ…Ш§ЩҶ Ш·ЩҲШұ Ъ©ЩҮ ШҜШұ ШҙЪ©Щ„ ЩҒЩҲЩӮ ЩҶШҙШ§ЩҶ ШҜШ§ШҜЩҮ ШҙШҜЩҮ Ш§ШіШӘ ШіЩҮ Ш®Ш· ШұШ§ ШЁШ§ ШҜЩҲ ШӘЩӮШ§Ш·Ш№ ШЁЩҮ ЩҮЩҒШӘ ЩӮШіЩ…ШӘ Щ…ЫҢ ШӘЩҲШ§ЩҶ ШӘЩӮШіЫҢЩ… Ъ©ШұШҜ.
ШҜЫҢЪҜШұВ Ш§ЪҜШұ ЪҜЩҲЫҢЩҶШҜ Ъ©ЩҮ Ш®ЩҲШ§ЩҮЫҢЩ… Ъ©ЩҮ ЪҶЩҮШ§Шұ ЩҫШ§ШұЩҮ ЪҶЩҲШЁ ШұШ§ ШЁЩҮ ЪҶЩҮШ§Шұ ШІШ®Щ… ШЁШұЫҢЩ… Ъ©ЩҮ ШҜЩҲШ§ШІШҜЩҮ ЩҫШ§ШұЩҮ ШҙЩҲШҜШҢ ЪҶЪҜЩҲЩҶЩҮ ШЁШ§ЫҢШҜ Ъ©ШұШҜЩҶШҹ Ш¬ЩҲШ§ШЁ ЪҜЩҲЫҢЫҢЩ… Ъ©ЩҮ Ш§ШІВ ЪҶЩҮШ§Шұ ЩҫШ§ШұЩҮ Щ…ШұШЁШ№ЫҢ ШіШ§ШІЫҢЩ… ЪҶЩҶШ§ЩҶ Ъ©ЩҮ ЪҶЩҮШ§Шұ ШӘЩӮШ§Ш·Ш№ ШЁШұ Ш§ЩҲ ЩҫЫҢШҜШ§ ШҙЩҲШҜ ШЁШұ Ш§ЫҢЩҶ Ъ©ШұШҜШ§Шұ Ъ©ЩҮ ЩҶЩ…ЩҲШҜЫҢЩ….В ЩҫШі ШЁЩҮ ЩҮШұ ШӘЩӮШ§Ш·Ш№ЫҢ ШІШ®Щ…ЫҢ ШЁШІЩҶЫҢЩ…ШҢ ШӘШ§ ШҜЩҲШ§ШІШҜЩҮ ЩҫШ§ШұЩҮ ШЁЫҢЩҒШӘШҜ ШЁШұ Ш§ЫҢЩҶ Ъ©ШұШҜШ§Шұ Ъ©ЩҮ ШЁЩҶЩ…ЩҲШҜЫҢЩ…:
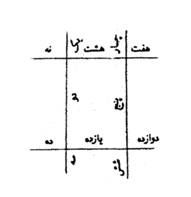
ШҜШұ Ш§ЫҢЩҶ Щ…ШіШҰЩ„ЩҮ Щ…Ш·Ш§ШЁЩӮ ШҙЪ©Щ„ ШЁШ§Щ„Ш§ ЪҶЩҮШ§Шұ Ш®Ш· ШұШ§ ШЁШ§ ЪҶЩҮШ§Шұ ЩҶЩӮШ·ЩҮ ШӘЩӮШ§Ш·Ш№ ШЁЩҮ ШҜЩҲШ§ШІШҜЩҮ ШЁШ®Шҙ ШӘЩӮШіЫҢЩ… Щ…ЫҢ Ъ©ЩҶЫҢЩ….
ШҜЫҢЪҜШұ Ш§ЪҜШұ ЪҜЩҲЫҢЩҶШҜ Ъ©ЩҮ Ш®ЩҲШ§ЩҮЫҢЩ… Ъ©ЩҮ ЩҫЩҶШ¬ ЩҫШ§ШұЩҮ ЪҶЩҲШЁ ШұШ§ ШЁЩҮ ЩҫЩҶШ¬ ШІШ®Щ… ЪҶЩҶШ§ЩҶ ШЁШЁШұЫҢЩ… Ъ©ЩҮ Ш§ШІ ЩҲЫҢ ЩҫШ§ЩҶШІШҜЩҮ ЩҫШ§ШұЩҮ ШӯШ§ШөЩ„ ШўЫҢШҜШҢ ЪҜЩҲЫҢЫҢЩ… Ъ©ЩҮ Ш§ШІ ШўЩҶ ЩҫЩҶШ¬ ЩҫШ§ШұЩҮ ЪҶЩҲШЁ ШұШ§ Щ…Ш®Щ…ШіЫҢ ШЁШіШ§ШІЫҢЩ… ШЁШұ Ш§ЫҢЩҶ Ъ©ШұШҜШ§Шұ Ъ©ЩҮ ШЁЩҶЩ…ЩҲШҜЫҢЩ… Ъ©ЩҮ ШҜШұ ЩҲЫҢ ЩҫЩҶШ¬ ШІШ®Щ… ШӘЩӮШ§Ш·Ш№ ШЁЩҲШҜ ЩҲ ШЁЩҮ ЩҮШұ ЩҶЩӮШ§Ш·ЫҢ ШІШ®Щ…ЫҢ ШЁШІЩҶЫҢЩ…ШҢ ЩҫШ§ЩҶШІШҜЩҮ ЩҫШ§ШұЩҮ ЪҜШұШҜШҜ. ЩҲ Ш¬Щ…Щ„ЩҮ ШЁШұ Ш§ЫҢЩҶ Ъ©ШұШҜШ§Шұ ШЁЩҲШҜ Ъ©ЩҮ ЫҢШ§ШҜ Ъ©ШұШҜЫҢЩ…:
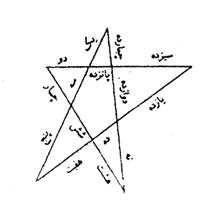
ШҜШұ Ш§ЫҢЩҶ Щ…ШіШҰЩ„ЩҮ ШЁШұ Ш·ШЁЩӮ ШҙЪ©Щ„ ШЁШ§Щ„Ш§ ЩҫЩҶШ¬ Ш®Ш· ШұШ§ ШЁШ§ ЩҫЩҶШ¬ ШӘЩӮШ§Ш·Ш№ ШЁЩҮ ЩҫШ§ЩҶШІШҜЩҮ ШЁШ®Шҙ ШӘЩӮШіЫҢЩ… Щ…ЫҢвҖҢЪ©ЩҶЫҢЩ….
ШҙЩҮШұШіШӘШ§ЩҶЫҢ Ш§ШіШӘ ЪҜШұШҜ ШЁШұ ЪҜШұШҜ ШўЩҶ ШҙЩҮШұШіШӘШ§ЩҶ ШҙШөШӘ ЩҒШұШіЩҶЪҜШҢ ЩҲ ШҜЩҲШ§ШІШҜЩҮВ ШҜШұЩҲШ§ШІШҜЩҮ ШҜШ§ШұШҜ. ЩҫШі ЩҫШ§ШҜШҙШ§ЩҮ ШўЩҶ ШҙЩҮШұ ЩҮЩҒШӘ ШЁШұЫҢШҜ ШұШ§ Ш§ШІ ШўЩҶ ШҙЩҮШұ ШЁЩҮ ШұШ§ЩҮ Ш§ЩҒЪҜЩҶШҜ.В ЩҶШ®ШіШӘЫҢЩҶ ШұШ§ ЪҜЩҒШӘ: ШӘЩҲ ЩҮШұ ШұЩҲШІ ЫҢЪ© ЩҒШұШіЩҶЪҜ ШЁШұЩҲ.В ШҜЩҲЩ… ШұШ§ ЪҜЩҒШӘ:В ЩҮШұ ШұЩҲШІ ШҜЩҲ ЩҒШұШіЩҶЪҜ ШЁШұЩҲ.В ШіЫҢЩ… ШұШ§ ЪҜЩҒШӘ:В ЩҮШұ ШұЩҲШІ ШіЩҮ ЩҒШұШіЩҶЪҜ ШЁШұЩҲ.В ЪҶЩҮШ§ШұЩ… ШұШ§ ЪҜЩҒШӘ ЩҮШұ ШұЩҲШІ ЪҶЩҮШ§Шұ ЩҒШұШіЩҶЪҜ ШЁШұЩҲ.В ЩҫЩҶШ¬Щ… ШұШ§ ЪҜЩҒШӘ ЩҮШұ ШұЩҲШІ ЩҫЩҶШ¬ ЩҒШұШіЩҶЪҜ ШЁШұЩҲ.В ШҙШҙЩ… ШұШ§ ЪҜЩҒШӘ:В ЩҮШұ ШұЩҲШІ ШҙШҙ ЩҒШұШіЩҶЪҜ ШЁШұЩҲ.В ЩҮЩҒШӘЩ… ШұШ§ ЪҜЩҒШӘ:В ЩҮШұ ШұЩҲШІ ЩҮЩҒШӘ ЩҒШұШіЩҶЪҜ ШЁШұЩҲ. Ш¬Щ…Щ„ЩҮ ЪҜШұШҜ ШҙЩҮШұ ШЁШұШўЫҢЫҢШҜ ШЁШұ Ш§ЫҢЩҶ Щ…ЩӮШҜШ§Шұ Ъ©ЩҮ ЪҜЩҒШӘЩ….В ЪҶЩҲЩҶ ЩҮШұ ЩҮЩҒШӘ ШЁЩҮ ШҜШұЩҲШ§ШІЩҮ ШұШіЫҢШҜ Щ…ШұШ§ Ш®ШЁШұ ШҜЩҮЫҢШҜ. .ШұЩҒШӘЩҶШҜ ЩҲ ЪҜШұШҜ ШЁШұ ЪҜШұШҜ ШҙЩҮШұ ШЁШұШўЩ…ШҜЩҶШҜ ЩҲ ШЁЩҮ ЫҢЪ© ШЁШ§Шұ ШЁЩҮ ШҜШұЩҲШ§ШІЩҮ ШұШіЫҢШҜЩҶШҜ.В ЩҫЫҢШҜШ§ ШЁШ§ЫҢШҜ Ъ©ШұШҜ Ъ©ЩҮ ЩҮШұ ЫҢЪ© ЪҶЩҶШҜ ШЁШ§Шұ ЪҜШұШҜ ШҙЩҮШұ ШЁШұШўЩ…ШҜЩҮ ШЁШ§ШҙЩҶШҜ ЩҲ ЩҮШұ ЫҢЪ© ШЁЩҮ ЪҶЩҶШҜ ШұЩҲШІ ШўЩҶШ¬Ш§ ШұШіЫҢШҜЩҮ ШЁШ§ШҙЩҶШҜ.
ЪҶЩҶШ§ЩҶ Ш§ШіШӘ Ъ©ЩҮ ШўЩҶ Щ…ШұШҜ Ъ©ЩҮ ЩҮШұ ШұЩҲШІ ЩҮЩҒШӘ ЩҒШұШіЩҶЪҜ ШұЩҒШӘШҢ ЪҶЩҮШ§ШұШҜЩҮ ШЁШ§Шұ ЪҜШұШҜ ШҙЩҮШұ ШЁШұШўЩ…ШҜЩҮ ШЁШ§ШҙШҜ ШЁЩҮ ШөШҜ ЩҲ ШЁЫҢШіШӘ ШұЩҲШІ.В ШўЩҶ Ъ©ЩҮ ЩҮШұ ШұЩҲШІ ШҙШҙ ЩҒШұШіЩҶЪҜ ШұЩҒШӘШҢ ШҜЩҲШ§ШІШҜЩҮ ШЁШ§Шұ ЪҜШұШҜ ШҙЩҮШұ ШЁШұ ШўЩ…ШҜЩҮ ШЁШ§ШҙШҜ ШЁЩҮ ШөШҜ ЩҲ ШЁЫҢШіШӘ ШұЩҲШІ.В ЩҲ ШўЩҶ Ъ©ЩҮ ЩҮШұ ШұЩҲШІ ЩҫЩҶШ¬ ЩҒШұШіЩҶЪҜ ШұЩҒШӘЩҮ ШЁШ§ШҙШҜ ШҜЩҮ ШЁШ§Шұ ЪҜШұШҜ ШҙЩҮШұ ШЁШұШўЩ…ШҜЩҮ ШЁШ§ШҙШҜ ШЁЩҮ ШөШҜ ЩҲ ШЁЫҢШіШӘ ШұЩҲШІ.В ЩҲ ШўЩҶ Ъ©ЩҮ ЩҮШұ ШұЩҲШІ ЪҶЩҮШ§Шұ ЩҒШұШіЩҶЪҜ ШұЩҒШӘЩҮ ШЁШ§ШҙШҜ ЩҮШҙШӘ ШЁШ§Шұ ШЁШұ ЪҜШұШҜ ШҙЩҮШұ ШЁШұШўЩ…ШҜ ШЁШ§ШҙШҜ ШЁЩҮ ШөШҜ ЩҲ ШЁЫҢШіШӘ ШұЩҲШІ.В ЩҲ ШўЩҶ Ъ©ЩҮ ЩҮШұ ШұЩҲШІ ШҜЩҲ ЩҒШұШіЩҶЪҜ ШұЩҒШӘЩҮ ШЁШ§ШҙШҜШҢ ЪҶЩҮШ§Шұ ШЁШ§Шұ ЪҜШұШҜ ШҙЩҮШұ ШЁШұШўЩ…ШҜЩҮ ШЁШ§ШҙШҜ ШЁЩҮ ШөШҜ ЩҲ ШЁЫҢШіШӘ ШұЩҲШІ.В ЩҲ ШўЩҶ Ъ©ЩҮ ЩҮШұ ШұЩҲШІ ЫҢЪ© ЩҒШұШіЩҶЪҜ ШұЩҒШӘЩҮ ШЁШ§ШҙШҜШҢ ШҜЩҲ ШЁШ§Шұ ЪҜШұШҜ ШҙЩҮШұ ШЁШұШўЩ…ШҜЩҮ ШЁШ§ШҙШҜ ШЁЩҮ ШөШҜ ЩҲ ШЁЫҢШіШӘ ШұЩҲШІ ШўЩҶШ¬Ш§ ШұШіЫҢШҜЩҮ ШЁШ§ШҙШҜ.
ШҜШұ Ш§ЫҢЩҶ Щ…Ш№Щ…Ш§ ЩҫШ§ШҜШҙШ§ЩҮЫҢ ЩҮЩҒШӘ ЩҫЫҢЪ© Ш®ЩҲШҜ ШұШ§ Ш§ШІ ШҜШұЩҲШ§ШІ ШҙЩҮШұЫҢ Ъ©ЩҮ ЩҫЫҢШұШ§Щ…ЩҲЩҶШҙ ШҙШөШӘ ЩҒШұШіЩҶЪҜ ШЁЩҲШҜЩҮ Ш§ШіШӘ Щ…ЫҢ ЩҒШұШіШӘШҜ ЩҲ ШЁЩҮ Ш§ЩҲЩ„ЫҢЩҶ ЩҫЫҢЪ© Щ…ЫҢ ЪҜЩҲЫҢШҜ ШұЩҲШІЫҢ ЫҢЪ© ЩҒШұШіЩҶЪҜ ШЁШұЩҲ ЩҲ ШЁЩҮ ЩҫЫҢЪ© ШҜЩҲЩ… ШӘШ§ ЩҮЩҒШӘЩ… ШЁЩҮ ШӘШұШӘЫҢШЁ Щ…ЫҢ ЪҜЩҲЫҢШҜ ШұЩҲШІЫҢ ШҜЩҲ ШӘШ§ ЩҮЩҒШӘ ЩҒШұШіЩҶЪҜ ШЁШұЩҲЩҶШҜ. Ш§ШІ ШўЩҶШ¬Ш§ЫҢЫҢ Ъ©ЩҮ ЩҫЫҢШұШ§Щ…ЩҲЩҶ ШҙЩҮШұ ШҙШөШӘ ЩҒШұШіЩҶЪҜ ШЁЩҲШҜЩҮ Ш§ШіШӘ ЩҲЩҮЩ…ЩҮ ШҜШұ ЫҢЪ© ШұЩҲШІ ШЁЩҮ ШўЩҶ ШҜШұЩҲШ§ШІЩҮ ШұШіЫҢШҜЩҮ Ш§ЩҶШҜШҢ ЩҶЩҒШұ Ш§ЩҲЩ„ Ъ©ЩҮ ШұЩҲШІЫҢ ЫҢЪ© ЩҒШұШіЩҶЪҜ Щ…ЫҢ ШұЩҒШӘЩҮ Ш§ШіШӘ ЩҫШі Ш§ШІ ШҙШөШӘ ШұЩҲШІ Щ…ЫҢ ШұШіШҜ ЩҲ ЪҶЩҲЩҶ ШЁЩӮЫҢЩҮ ЩҮЩ… Щ…Ш§ЩҶЩҶШҜ ЩҫЫҢЪ© Ш§ЩҲЩ„ ЩҫШі Ш§ШІ ШҙШөШӘ ШұЩҲШІ Щ…ЫҢ ШұШіЩҶШҜШҢВ ШЁЩҶШ§ШЁШұШ§ЫҢЩҶ ШіШұШ№ШӘ ШўЩҶЩҮШ§ ШЁЩҮ ШӘШұШӘЫҢШЁ ШҜЩҲ ШӘШ§ ЩҮЩҒШӘ ШЁШұШ§ШЁШұ Ш§ЩҲ ШЁЩҲШҜЩҮ Ш§ШіШӘ ШӘШ§ ШӘЩҲШ§ЩҶШіШӘЩҮ Ш§ЩҶШҜ ЩҮЩ…ШІЩ…Ш§ЩҶ ШЁШ§ Ш§ЩҲ ШЁЩҮ ШўЩҶШ¬Ш§ ШЁШұШіЩҶШҜ. ЫҢШ№ЩҶЫҢ ЩҶЩҒШұ ШҜЩҲЩ… ШӘШ§ ЩҮЩҒШӘЩ… ШЁЩҮ ШӘШұШӘЫҢШЁ ШҜЩҲШҢ ШіЩҮШҢ ЪҶЩҮШ§ШұШҢ ЩҫЩҶШ¬ШҢ ШҙШҙШҢ ЩҲ ЩҮЩҒШӘ ШҜЩҲШұ ШҜЩҲШұ ШҙЩҮШұ ЪҜШҙШӘЩҮ Ш§ШіШӘ Ъ©ЩҮ Ш§ЪҜШұ ЩҮШұ ШҜЩҲШұ ШұШ§ ШҙШөШӘ ЩҒШұШіЩҶЪҜ ШӯШіШ§ШЁ Ъ©ЩҶЫҢЩ… Щ…ШіШ§ЩҒШӘ Ш·ЫҢ ШҙШҜЩҮ ШӘЩҲШіШ· ЩҮШұЫҢЪ© ШЁЩҮ ШӘШұШӘЫҢШЁ ШЁЩҮ ШҜШіШӘ Щ…ЫҢ ШўЫҢШҜ. Ш§Щ…Ш§ Ш·ШЁШұЫҢ ШҜШұ ШӘЩҲШ¶ЫҢШӯ Щ…ШіШҰЩ„ЩҮ ШЁШұШ§ЫҢ ЩҫЫҢЪ© Ш§ЩҲЩ„ ШҜЩҲ ШҜЩҲШұ ШӯШіШ§ШЁ Ъ©ШұШҜЩҮ Ш§ШіШӘ ЩҲ ШЁЩҶШ§ШЁШұШ§ЫҢЩҶ ШӘШ№ШҜШ§ШҜ ШҜЩҲШұЩҮШ§ ЩҲ Щ…ШіШ§ЩҒШ§ШӘ ШЁШұШ§ЫҢ ШЁЩӮЫҢЩҮ ЩҫЫҢЪ©вҖҢЩҮШ§ ШҜЩҲШЁШұШ§ШЁШұ ШҙШҜЩҮ Ш§ШіШӘ.
ШҜЫҢЪҜШұ ШіЩҮ ЪҜЩҲЩҶЩҮ ШЁЩҶЪҜШ§ЩҮ Ш§ШіШӘ Щ…Ш®Ш§Щ„ЩҒ ЫҢЪ©ЫҢ ШҜЩҮ ЩҫШ§ШұЩҮ ЩҲ ЫҢЪ©ЫҢ ШіЫҢ ЩҫШ§ШұЩҮ ЩҲ ЫҢЪ©ЫҢ ЩҫЩҶШ¬Ш§ЩҮ ЩҫШ§ШұЩҮШҢ Щ…ЫҢ ШЁШ§ЫҢШҜ ЩҒШұЩҲШ®ШӘ. ЩҮШұ ШіЩҮ ЪҜЩҲЩҶЩҮ ШЁЩҮ ЫҢЪ© ЩҶШұШ® ЪҶЩҶШ§ЩҶ Ъ©ЩҮ ШўЩҶ ЩҮШұ ШіЩҮ ЪҜЩҲЩҶЩҮ ШұШ§ШіШӘ Ш§ШіШӘ ШЁЩҮ ЩҮЩ… ШЁЩҮШ§ ШўЫҢШҜ. ЩҫЫҢШҜШ§ ШЁШ§ЫҢШҜ Ъ©ШұШҜЩҶ Ъ©ЩҮ ЪҶЪҜЩҲЩҶЩҮ ЩҒШұЩҲШ®ШӘЩҮ ШўЫҢШҜШҢ Ъ©ЩҮ Ш§ЪҜШұ ЫҢЪ©ЫҢ ЩҫШ§ШұЩҮ Ш§ШІ Ъ©Щ…ШӘШұЫҢЩҶ ШЁЩҮ ШҜШұЩ…ЫҢ ШҜЩҮШҜШҢ Ш¬Щ…Щ„ЩҮ ШұШ§ ШҜЩҮ ШҜШұЩ… ШӯШ§ШөЩ„ ШўЫҢШҜ. ЩҲ ШўЩҶ ШіЫҢ ЩҫШ§ШұЩҮ ШұШ§ ЩҶЫҢШІ ЩҮШұ ЫҢЪ©ЫҢ ШұШ§ ШЁЩҮ ШҜШұЩ…ЫҢ ШЁШ§ЫҢШҜ ЩҒШұЩҲШ®ШӘШҢ ШіЫҢ ШҜШұЩ… ШӯШ§ШөЩ„ ШўЫҢШҜ. ЩҲ ШўЩҶ ЩҫЩҶШ¬Ш§ЩҮ ЩҫШ§ШұЩҮ ЩҮШұ ЫҢЪ©ЫҢ ШЁЩҮ ШҜШұЩ…ЫҢ ШЁШ§ЫҢШҜ ЩҒШұЩҲШ®ШӘШҢ ЩҫЩҶШ¬Ш§ЩҮ ШҜШұЩ… ШӯШ§ШөЩ„ ШўЫҢШҜ ЩҲ ШЁШ§ ЫҢЪ©ШҜЫҢЪҜШұ ШұШ§ШіШӘ ЩҶШЁШ§ШҙШҜ ЩҲ Ъ©Щ…ШӘШұЫҢЩҶ ЩҮШұ ШҜЩҮ ШЁЩҮ ШҜШұЩ…ЫҢ ШҜЩҮШҜШҢ ШўЩҶ ШіЫҢ ШұШ§ ЩҶЫҢШІ ЩҮШұ ШҜЩҮ ШЁЩҮ ШҜШұЩ…ЫҢ ШҜЩҮШҜШҢ ШіЩҮ ШҜШұЩ… ШЁШ§ШҙШҜ.В ЩҲ ЩҫЩҶШ¬Ш§ЩҮ ШұШ§ ЩҫЩҶШ¬ ШҜШұЩ… ШЁЩҮ ЩҮЩ… ШұШ§ШіШӘ ЩҶШЁШ§ШҙШҜ.В ЩҲШ¬ЩҮШҙ ШўЩҶ Ш§ШіШӘ Ъ©ЩҮ ЪҶЩҲЩҶ Щ…ШҙШӘШұЫҢ ШЁЫҢШ§ЫҢШҜШҢ ЩҒШұЩҲШҙЩҶШҜЩҮ ЪҜЩҲЫҢШҜ:В ЩҮШұ ЩҮЩҒШӘЫҢ ШұШ§ Ъ©ЩҮ Ш§ЩҶШҜШұ Ш§ЫҢШҙШ§ЩҶ Ш§ШіШӘ ШЁЩҮ ШҜШұЩ…ЫҢ ШҜЩҮЩ…ШҢ ЩҲ ЩҮШұ ЪҶЩҮ Ш§ШІ ЩҮЩҒШӘ ШЁШ§ШІ Щ…Ш§ЩҶШҜШҢ ЩҮШұ ЫҢЪ©ЫҢ ШЁЩҮ ШіЩҮ ШҜШұЩ… ШҜЩҮЩ…. ЪҶЩҲЩҶ ЪҶЩҶЫҢЩҶ Ъ©ЩҶШҜШҢ ШЁЩҮШ§ ЩҲ ЩҶШұШ® ШұШ§ШіШӘШ§Шұ Ш§ШіШӘ ШЁШ§ЫҢШҜ ЪҶЩҶШ§ЩҶ Ъ©ЩҮ ШҜЩҮ ЩҫШ§ШұЩҮ ШұШ§ ЩҮЩҒШӘ ШЁЩҮ ШҜШұЩ…ЫҢ ШҜЩҮШҜШҢ ШіЩҮ ШЁЩ…Ш§ЩҶШҜ ШЁЩҮ ШіЩҮ ШҜШұЩ… ШҜЩҮШҜШҢ ЩҮШұ ЫҢЪ© ШҜЩҮ ШҜШұЩ… ШӯШ§ШөЩ„ ШўЫҢШҜ.В ЩҲ ШіЫҢ ЩҫШ§ШұЩҮ ШұШ§ ЩҮШұ ЩҮЩҒШӘ ШЁЩҮ ШҜШұЩ…ЫҢ ШҜЩҮШҜШҢ ЪҶЩҮШ§Шұ ЩҮЩҒШӘ ШұШ§ ЪҶЩҮШ§Шұ ШӯШ§ШөЩ„ ШўЫҢШҜШҢ ЩҲ ШЁЩ…Ш§ЩҶШҜ ШЁШ§ЩӮЫҢ ЩҮШұ ЫҢЪ© ШЁЩҮ ШіЩҮ ШҜШұЩ… ШҜЩҮШҜШҢ ШҙШҙ Ш¬Щ…Щ„ЩҮ ШҜЩҮ ШҜШұЩ… ШӯШ§ШөЩ„ ШўЫҢШҜ. ЩҲ ЩҫЩҶШ¬Ш§ЩҮ ШұШ§ ЩҮЩҒШӘ ШЁЩҮ ЫҢЪ© ШҜШұЩ… ШҜЩҮШҜ ЩҮЩҒШӘ ШЁШ§Шұ ЩҮЩҒШӘ ШҜШұЩ… ШӯШ§ШөЩ„ ШўЫҢШҜШҢ ЫҢЪ©ЫҢ Ш§ШІ ЩҫЩҶШ¬Ш§ЩҮ ШЁЩ…Ш§ЩҶШҜШҢ ШЁЩҮШ§ ШіЩҮ ШҜШұЩ…ШҢ Ш¬Щ…Щ„ЩҮ ШҜЩҮ ШҜШұЩ… ШЁШ§ШҙШҜ. ЩҮШұ ШіЩҮ ШЁЩҮШ§ ШЁЩҮ ЩҮЩ… ШұШ§ШіШӘ ШЁШ§ШҙШҜ.
ШіЩҮ ЩӮШ·Ш№ЩҮ ШІЩ…ЫҢЩҶ ЫҢШ§ Щ…Щ„Ъ© ЩҲШ¬ЩҲШҜ ШҜШ§ШұШҜ Ъ©ЩҮ Ъ©ЩҮ ЫҢЪ©ЫҢ ШҜЩҮ ЩӮШіЩ…ШӘ (ЫҢШ§ ШҜШ§ЩҶЪҜ) ЩҲ ШҜЫҢЪҜШұЫҢ ШіЫҢ ЩӮШіЩ…ШӘ ЩҲ ШіЩҲЩ…ЫҢ ЩҫЩҶШ¬Ш§ЩҮ ЩӮШіЩ…ШӘ Ш§ШіШӘ. Щ…ЫҢвҖҢШ®ЩҲШ§ЩҮЫҢЩ… ЩҮШұ ЫҢЪ© Ш§ШІ Ш§ЫҢЩҶ ШіЩҮ Щ…Щ„Ъ© ШұШ§ ШЁЩҮ ШҜЩҮ ШҜШұЩҮЩ… ШЁЩҒШұЩҲШҙЫҢЩ…ШҢ ШЁШҜЩҲЩҶ ШўЩҶ Ъ©ЩҮ Ш§ШІ Ш№ШҜШҜ Ъ©ШіШұЫҢ Ш§ШіШӘЩҒШ§ШҜЩҮ Ъ©ЩҶЫҢЩ… ЩҲ ЩҲШ§ШӯШҜ ЩҮШ§ ЩҮЩ…ЪҜЫҢ ШЁЩҮ ШҜШұЩҮЩ… ШЁШ§ШҙЩҶШҜ ЩҲ ШӘЩӮШіЫҢЩ… ЩҶШҙЩҲЩҶШҜ ЩҲ ЩҲШ§ШӯШҜ ЩҮШ§ ШұШ§ ЩҮЩ… ШЁЩҮ Ш·ЩҲШұ Щ…ШіШӘЩӮЩ„ ШЁЩҒШұЩҲШҙЫҢЩ…. ШұШ§ЩҮ ШӯЩ„ ШўЩҶ Ш§ЫҢЩҶ Ш§ШіШӘ Ъ©ЩҮ ЩҮШұ ЩҮЩҒШӘ ЩҫШ§ШұЩҮ Ш§ШІ Ш§ЫҢЩҶ Ш§Щ…Щ„Ш§Ъ© ШұШ§ ШЁЩҮ ЫҢЪ© ШҜШұЩҮЩ… ЩҲ ЩҮШұ ЫҢЪ© ЩҫШ§ШұЩҮ ШЁШ§ЩӮЫҢЩ…Ш§ЩҶШҜЩҮ ШұШ§ ШЁЩҮ ШіЩҮ ШҜШұЩҮЩ… ШЁЩҒШұЩҲШҙЫҢЩ…. ШЁЩҮ Ш§ЫҢЩҶ ШӘШұШӘЫҢШЁ ШЁШ§ЫҢШҜ Щ…Щ„Ъ© ШҜЩҮ ЩҫШ§ШұЩҮ ШұШ§ ЩҮШұ ЩҮЩҒШӘ ЩӮШіЩ…ШӘШҙ ШұШ§ ШЁЩҮ ЫҢЪ© ШҜШұ ЩҮЩ… ШЁЩҒШұЩҲШҙЫҢЩ… ЩҲ ЩҮШұ ШіЩҮ ЩҫШ§ШұЩҮ ШЁШ§ЩӮЫҢЩ…Ш§ЩҶШҜЩҮ ШұШ§ ШЁЩҮ ШіЩҮ ШҜШұЩҮЩ… ШЁЩҒШұЩҲШҙЫҢЩ…. ШҜШұ Ш§ЫҢЩҶ ШӯШ§Щ„ШӘ ШЁШұШ§ЫҢ ЩҮЩҒШӘ ЩӮШіЩ…ШӘ ЫҢЪ© ШҜШұЩҮЩ… ЩҲ ШЁШұШ§ЫҢ ШіЩҮ ЩӮШіЩ…ШӘ ШЁШ§ЩӮЫҢЩ…Ш§ЩҶШҜЩҮ Ъ©ЩҮ ЩҮШұ ЩӮШіЩ…ШӘ ШұШ§ ШіЩҮ ШҜШұЩҮЩ… ЩҒШұЩҲШ®ШӘЩҮвҖҢШ§ЫҢЩ… ЩҶЩҮ ШҜШұЩҮЩ… ШЁЩҮ ШҜШіШӘ Щ…ЫҢ ШўЩҲШұЫҢЩ… Ъ©ЩҮ ШҜШұ Щ…Ш¬Щ…ЩҲШ№ Ш§ЫҢЩҶ Щ…Щ„Ъ© ШҜЩҮ ЩҫШ§ШұЩҮ ШұШ§ ШЁЩҮ ШҜЩҮ ШҜШұЩҮЩ… ЩҒШұЩҲШ®ШӘЩҮ Ш§ЫҢЩ…. ШЁШұШ§ЫҢ Щ…Щ„Ъ© ШіЫҢ ЩҫШ§ШұЩҮ ЩҮШұ ЩҮЩҒШӘ ЩҫШ§ШұЩҮ ШұШ§ ШЁЩҮ ЫҢЪ© ШҜШұЩҮЩ… Щ…ЫҢ ЩҒШұЩҲШҙЫҢЩ… Ъ©ЩҮ ШҜШұ Ш§ЫҢЩҶ ШӯШ§Щ„ ШЁШұШ§ЫҢ ШЁЫҢШіШӘ ЩҲ ЩҮШҙШӘ ЩҫШ§ШұЩҮ ЪҶЩҮШ§Шұ ШҜШұЩҮЩ… ШЁЩҮ ШҜШіШӘ Щ…ЫҢвҖҢШўЩҲШұЫҢЩ… ЩҲ ШҜЩҲ ЩҫШ§ШұЩҮ ШЁШ§ЩӮЫҢЩ…Ш§ЩҶШҜЩҮ ШұШ§ ЩҮШұ ЩҫШ§ШұЩҮ ШЁЩҮ ШіЩҮ ШҜШұЩҮЩ… Щ…ЫҢ ЩҒШұЩҲШҙЫҢЩ… Ъ©ЩҮ ШҙШҙ ШҜШұЩҮЩ… Щ…ЫҢ ШҙЩҲШҜ ЩҲ ШҜШұ Щ…Ш¬Щ…ЩҲШ№ ШҜЩҮ ШҜШұЩҮЩ… Ш§ШІ ЩҒШұЩҲШҙ Ш§ЫҢЩҶ ШіЫҢ ЩҫШ§ШұЩҮ ШӯШ§ШөЩ„ ШҙШҜЩҮ Ш§ШіШӘ. ШЁШұШ§ЫҢ Щ…Щ„Ъ© ЩҫЩҶШ¬Ш§ЩҮ ЩҫШ§ШұЩҮ ЩҮШұ ЩҮЩҒШӘ ЩҫШ§ШұЩҮ ШұШ§ ШЁЩҮ ЫҢЪ© ШҜШұЩҮЩ… Щ…ЫҢвҖҢЩҒШұЩҲШҙЫҢЩ… ЩҲ ЩҮЩҒШӘ ШҜШұЩҮЩ… ШЁЩҮ ШҜШіШӘ Щ…ЫҢ ШўЩҲШұЫҢЩ… ЩҲ ЫҢЪ© ЩҫШ§ШұЩҮ ШЁШ§ЩӮЫҢЩ…Ш§ЩҶШҜЩҮ ШұШ§ ЩҮЩ… ШЁЩҮ ШіЩҮ ШҜШұЩҮЩ… Щ…ЫҢ ЩҒШұЩҲШҙЫҢЩ… ЩҲ ШҜЩҮ ШҜШұЩҮЩ… ШЁЩҮ ШҜШіШӘ Щ…ЫҢвҖҢШўЩҲШұЫҢЩ….
ШҜЫҢЪҜШұ ШіЩҮ Щ…ШұШҜ ШЁШ§ ЩҮЩ… ШЁЩҮ ШұШ§ЩҮЫҢ Щ…ЫҢ ШұЩҒШӘЩҶШҜ. ШЁШ§ ЫҢЪ©ЫҢ ШіЩҮ ЩҶШ§ЩҶ ШЁЩҲШҜ. Щ…ЫҢ ШұЩҒШӘЩҶШҜ. ШЁШ§ ЫҢЪ©ЫҢ ШҜЩҲ ЩҶШ§ЩҶ ЩҲ ШЁШ§ ШіЩҲЩ… ЩҮЫҢЪҶ ЩҶШЁЩҲШҜ. ШҜШұ ЩҲЩӮШӘ ЪҶЫҢШІЫҢ Ш®ЩҲШұШҜЩҶ ШЁЩҮ ЫҢЪ© Ш¬Ш§ ЩҶШҙШіШӘЩҶШҜ ЩҲ ШўЩҶ ЩҫЩҶШ¬ ЩҶШ§ЩҶ ШЁШ§ ЩҮЩ… ШЁШ®ЩҲШұШҜЩҶШҜ ЪҶЩҶШ§ЩҶ Ъ©ЩҮ ЩҮЫҢЪҶ ЩҶЩ…Ш§ЩҶШҜ. ШўЩҶ Щ…ШұШҜ Ъ©ЩҮ ЩҶШ§ЩҶ ЩҶШҜШ§ШҙШӘ ЪҜЩҒШӘ Ъ©ЩҮ ЩҶШ§ЩҶ ШҙЩ…Ш§ ЪҶЩҶШҜ ШЁЩҲШҜШҹ ЪҜЩҒШӘЩҶШҜ: ЩҫЩҶШ¬ ЩҶШ§ЩҶ. ШўЩҶ Щ…ШұШҜ ЩҫЩҶШ¬ ШҜШұЩ… ШЁЩҮ ШўЩҶ ШҜЩҲ Щ…ШұШҜ ШҜШ§ШҜ ЩҲ ЪҜЩҒШӘ ЩҮШұ ЫҢЪ© ШЁЩҮШ§ЫҢ ЩҶШ§ЩҶ Ш®ЩҲШҜ ШұШ§ ШЁШұШҜШ§ШұШҜ. ШўЩҶ Ъ©Ші Ъ©ЩҮ ШҜЩҲ ЩҶШ§ЩҶ ШҜШ§ШҙШӘШҢ ЪҜЩҒШӘ ШўЩҶ ШҜЫҢЪҜШұ ШұШ§ Ъ©ЩҮ ШӘЩҲ ШіЩҮ ЩҶШ§ЩҶ ШҜШ§ШҙШӘЫҢШҢ ШіЩҮ ШҜШұЩ… ШЁШұШҜШ§Шұ ЩҲ Щ…ЩҶ ШҜЩҲ ЩҶШ§ЩҶ ШҜШ§ШҙШӘЩ…ШҢ ШҜЩҲ ШҜШұЩ… ШЁШұШҜШ§ШұЩ…. Ш®ШҜШ§ЩҲЩҶШҜ ШіЩҮ ЩҶШ§ЩҶ ЪҜЩҒШӘ Щ…ШұШ§ ШЁЫҢШҙ Щ…ЫҢ ШұШіШҜ ЩҲ Щ…ЫҢШ§ЩҶШҙШ§ЩҶ ШҜШ§ЩҲШұЫҢ Ш®Ш§ШіШӘ.В ЩҫШі ЩҫЫҢШҜШ§ ШЁШ§ЫҢШҜ Ъ©ШұШҜ Ъ©ЩҮ ЩҮШұ ЫҢЪ© ШұШ§ ЪҶЩҮ ШұШіШҜ. ШҙЩ…Ш§Шұ ШўЩҶ Ш§ШіШӘ Ъ©ЩҮ ШўЩҶ Ъ©ЩҮ ШіЩҮ ЩҶШ§ЩҶ ШҜШ§ШҙШӘШҢ ЪҶЩҮШ§Шұ ШҜШұЩ… ШЁШұЪҜЫҢШұШҜШҢ ЩҲ ШўЩҶ Ъ©ЩҮ ШҜЩҲ ЩҶШ§ЩҶ ШҜШ§ШҙШӘШҢ ШҜШұЩ…ЫҢ.В Ш§ШІ ШЁЩҮШұ ШўЩҶ Ъ©ЩҮ Ш§ЫҢШҙШ§ЩҶ ЩҶШ§ЩҶ ШЁЩҮ ЩҮЩ… Ш®ЩҲШұШҜЩҶШҜ ШұШ§ШіШӘШҢ ЪҶЩҮШ§Шұ ШіЩҮ ЫҢЪ© ЩҶШ§ЩҶ ШўЩҶ Ъ©ШіЫҢ Ъ©ЩҮ ШіЩҮ ЩҶШ§ЩҶ ШҜШ§ШҙШӘ Ш§ЫҢЩҶ Щ…ШұШҜ Ш®ЩҲШұШҜЩҮ Ш§ШіШӘ ЩҲ ШіЩҮ ШҜЫҢЪҜШұ ШўЩҶ Ъ©ЩҮ ШҜЩҲ ЩҶШ§ЩҶ ШҜШ§ШҙШӘ ЩҲ ШўЩҶ Щ…ШұШҜ Ъ©ЩҮ ШҜШұЩ… ШҜШ§ШұШҜШҢ ЩҫЩҶШ¬ ШіЩҮ ЫҢЪ© Ш®ЩҲШұШҜЩҮ Ш§ШіШӘ ЩҲ ЩҫЩҶШ¬ ШҜШұЩ… ШҜШ§ШҜЩҮ.В ЩҮШұ ШіЩҮ ЫҢЪ©ЫҢ ШұШ§ ШҜШұЩ…ЫҢ ШұШіШҜ.В ЪҶЩҮШ§Шұ ШіЩҮ ЫҢЪ© ШұШ§ШҢ ЪҶЩҮШ§Шұ ШҜШұЩ… ШұШіШҜ ЩҲ ШіЩҮ ЫҢЪ©ЫҢ ШұШ§ ШҜШұЩ…ЫҢ ЩҲ ШҙЩ…Ш§Шұ ШЁШұ Ш§ЫҢЩҶ Ъ©ШұШҜШ§Шұ ШЁЩҲШҜ.
ШҜШұ Ш§ЫҢЩҶ Щ…ШіШҰЩ„ЩҮ ШҜЩҲ ЩҮЩ…ШіЩҒШұ Ъ©ЩҮ ЫҢЪ©ЫҢ ШіЩҮ ЩҶШ§ЩҶ ЩҲ ШҜЫҢЪҜШұЫҢ ШҜЩҲ ЩҶШ§ЩҶ ШҜШ§ШҙШӘЩҶШҜ ЩҫЩҶШ¬ ЩҶШ§ЩҶ ШұШ§ Щ…ЫҢШ§ЩҶ Ш®ЩҲШҜ ЩҲ Щ…ЫҢЩҮЩ…Ш§ЩҶШҙШ§ЩҶ ШЁЩҮ Ш·ЩҲШұ Щ…ШіШ§ЩҲЫҢ Ш®ЩҲШұШҜЩҶШҜ. Щ…ЫҢЩҮЩ…Ш§ЩҶ ЩҫЩҶШ¬ ШҜШұЩҮЩ… ШЁЩҮ ШўЩҶЩҮШ§ Щ…ЫҢ ШҜЩҮШҜ. ШўЩҶ Ъ©Ші Ъ©ЩҮ ШҜЩҲ ЩҶШ§ЩҶ ШҜШ§ШҙШӘ ЪҜЩҒШӘ ШҜЩҲ ШҜШұЩҮЩ… Щ…Ш§Щ„ Щ…ЩҶ ЩҲ ШіЩҮ ШҜШұЩҮЩ… Щ…Ш§Щ„ ШӘЩҲ Ъ©ЩҮ ШіЩҮ ЩҶШ§ЩҶ ШҜШ§ШҙШӘЫҢ. Ш§Щ…Ш§ ШўЩҶ Щ…ШұШҜ ЪҜЩҒШӘ ШЁЩҮ Щ…ЩҶ ШіЩҮЩ… ШЁЫҢШҙШӘШұЫҢ Щ…ЫҢ ШұШіШҜ. Ш§Щ„ШЁШӘЩҮ Ш§ЩҲ ШҜШұШіШӘ Щ…ЫҢ ЪҜЩҒШӘ. ЪҶЩҲЩҶ Ш§ЩҲ ШЁШ§ЫҢШҜ ЪҶЩҮШ§Шұ ШҜШұЩҮЩ… ЩҲ Щ…ШұШҜЫҢ Ъ©ЩҮ ШҜЩҲ ЩҶШ§ЩҶ ШҜШ§ШҙШӘ ЫҢЪ© ШҜШұЩҮЩ… ШЁШұШҜШ§ШұШҜ. ЪҶЩҲЩҶ ЩҫЩҶШ¬ ЩҶШ§ЩҶ Щ…ЫҢШ§ЩҶ ШіЩҮ ЩҶЩҒШұ ШЁЩҮ ЩӮШіЩ…ШӘ Щ…ШіШ§ЩҲЫҢ ШӘЩӮШіЫҢЩ… ШҙШҜЩҮ ШЁЩҲШҜШҢ ШЁЩҶШ§ШЁШұШ§ЫҢЩҶ ЩҫШ§ЩҶШІШҜЩҮ ШӘЪ©ЩҮ ЩҶШ§ЩҶ ШЁЩҲШҜЩҮ Ш§ШіШӘВ Ъ©ЩҮ ЩҮШұ Ъ©ШҜШ§Щ… Ш§ШІ Ш§ЫҢЩҶ ШіЩҮ ЩҶЩҒШұ ЩҫЩҶШ¬ ШӘЪ©ЩҮ ЩҶШ§ЩҶ ШұШ§ Ш®ЩҲШұШҜЩҮ Ш§ШіШӘ. Щ…ЫҢЩҮЩ…Ш§ЩҶ ЩҫЩҶШ¬ ШҜШұЩҮЩ… Щ…ЫҢ ШҜЩҮШҜ ЩҲ ЩҮШұЫҢЪ© Ш§ШІ ШўЩҶ ШҜЩҲ ШөШ§ШӯШЁ ЩҶШ§ЩҶ ШЁШ§ЫҢШҜ ШЁЩҮ ШӘШұШӘЫҢШЁ ЩҮШІЫҢЩҶЩҮ ЩҫЩҶШ¬ ШіЩҲЩ… ШіЩҮ ЩҶШ§ЩҶ ЩҲ ЩҫЩҶШ¬ ШіЩҲЩ… ШҜЩҲЩҶШ§ЩҶ ШұШ§ ШЁЪҜЫҢШұЩҶШҜ. Щ…ЫҢШІШЁШ§ЩҶ Ъ©ЩҮ ЩҶШ§ЩҶЫҢ ЩҶШҜШ§ШҙШӘЩҮ Ш§ШіШӘ ЩҲ ЩҫЩҶШ¬ ШіЩҲЩ… ЩҶШ§ЩҶ ШұШ§ Ш®ЩҲШұШҜЩҮ Ш§ШіШӘШҢ ЩҫЩҶШ¬ ШҜШұ ЩҮЩ… Щ…ЫҢ ШҜЩҮШҜ. ШЁЩҮШ§ЫҢ ЫҢЪ© ШӘЪ©ЩҮ Ш§ШІ ЩҶШ§ЩҶ ШұШ§ ШЁЩҮ ШҙШ®ШөЫҢ Ъ©ЩҮ ШҜЩҲ ЩҶШ§ЩҶ ШҜШ§ШҙШӘЩҮ Ш§ШіШӘ ЩҲ ШЁЩҮШ§ЫҢ ЪҶЩҮШ§Шұ ШӘЪ©ЩҮ Ш§ШІ ЩҶШ§ЩҶ ШұШ§ ШЁЩҮ ШҙШ®ШөЫҢ Ъ©ЩҮ ШіЩҮ ЩҶШ§ЩҶ ШҜШ§ШҙШӘЩҮ Ш§ШіШӘ..
ШұШ§ЩҮ ШӯЩ„ ШұЫҢШ§Ш¶ЫҢ Ш§ЫҢЩҶ Щ…ШіШҰЩ„ЩҮ ЪҶЩҶЫҢЩҶ Ш§ШіШӘ :
В В В В В В В В В В 3-5/3=4/3В В В В
В В В В В В В 2-5/3=1/3В
В ЩҶЩҒШұ ШҜЩҲЩ… ШЁШ§ЫҢШҜ ШЁЩҮ Ш§ЫҢЩҶ Щ…ЩӮШҜШ§Шұ ЩҫЩҲЩ„ ШЁЪҜЫҢШұШҜ:
: ЩҶЩҒШұ ШіЩҲЩ… Ъ©ЩҮ ЩҶШ§ЩҶЫҢ ЩҶШҜШ§ШҙШӘЩҮ Ш§ШіШӘ ЩҫЩҶШ¬ ШҜШұЩҮЩ… ШЁЩҮ Ш§ШІШ§ЫҢ ЩҫЩҶШ¬ ШіЩҲЩ… ЩҶШ§ЩҶЫҢ Ъ©ЩҮ Ш®ЩҲШұШҜЩҮ Ш§ШіШӘ Щ…ЫҢ ШҜЩҮШҜ
В 0-5/3=-5/3
ШЁЩҶШ§ШЁШұШ§ЫҢЩҶ ЩҶЩҒШұ Ш§ЩҲЩ„ ШЁШ§ Ш§ЫҢЩҶ ШӯШіШ§ШЁ ШЁШ§ЫҢШҜ ЪҶЩҮШ§Шұ ШҜШұЩҮЩ… ШЁЪҜЫҢШұШҜ
(4/3*5)/(5/3)=4/3*5*3/5=4
ЩҲ ЩҶЩҒШұ ШҜЩҲЩ… ШЁШ§ Ш§ЫҢЩҶ ШӯШіШ§ШЁ ШЁШ§ЫҢШҜ ЫҢЪ© ШҜШұЩҮЩ… ШЁЪҜЫҢШұШҜ:
(1/3*5)/(5/3)=1/3*5*3/5=1В
Ш§ЫҢЩҶ Щ…ШіШҰЩ„ЩҮ ШұШ§ ШЁЩҮ ШҙЫҢЩҲЩҮ ШҜЫҢЪҜШұЫҢ ЩҶЫҢШІ Щ…ЫҢвҖҢШӘЩҲШ§ЩҶ ШӯЩ„ Ъ©ШұШҜ Ъ©ЩҮ ШЁШұШ§ЫҢВ Ш§Ш®ШӘШөШ§Шұ ШўЩҶ ШұШ§ ЩҶЩ…ЫҢ ШўЩҲШұЫҢЩ….
ШҜЫҢЪҜШұ ЩҫШ§ШҜШҙШ§ЩҮ ШўЩҶ ШҜЩҲ ШҙЩҮШұ Щ…Ш®ШӘЩ„ЩҒ ШҜЩҲ ШұШіЩҲЩ„ ЩҒШұШіШӘШ§ШҜЩҶШҜ ШЁЩҮ ЫҢЪ©ШҜЫҢЪҜШұ. ЫҢЪ© ЩҫШ§ШҜШҙШ§ЩҮ ШұШіЩҲЩ„ Ш®ЩҲШҜ ШұШ§ ЪҜЩҒШӘ: ЩҮШұ ШұЩҲШІ ЩҮШҙШӘ ЫҢЪ©ЫҢ Ш¬Щ…Щ„ЩҮ Ш§ШІ Ш§ЫҢЩҶ ШұШ§ЩҮ ШҙЩҮШұ ШӘШ§ ШЁШҜШ§ЩҶ ШҙЩҮШұ Щ…ЫҢ ШұЩҲ.В ЩҲ ШўЩҶ ШҜЫҢЪҜШұ ЩҫШ§ШҜШҙШ§ЩҮ ШұШіЩҲЩ„ Ш®ЩҲШҜ ШұШ§ ЪҜЩҒШӘ:В ЩҮШұ ШұЩҲШІ ШҜЩҮ ЫҢЪ©ЫҢ Ш§ШІ Ш§ЫҢЩҶ ШұШ§ЩҮ ШҙЩҮШұ ШӘШ§ ШўЩҶ ШҙЩҮШұ ШҜЫҢЪҜШұ Щ…ЫҢ ШұЩҲ. Ш§Ъ©ЩҶЩҲЩҶ ШЁШЁШ§ЫҢШҜ ЪҜЩҒШӘ Ъ©ЩҮ Ш§ШІ Ш§ЫҢЩҶ ШҙЩҮШұ ШЁШҜШ§ЩҶ ШҙЩҮШұ ЪҶЩҶШҜ ЩҒШұШіЩҶЪҜ ШЁЩҲШҜЩҮ Ш§ШіШӘ ЩҲ ЩҮШұ ШұЩҲШІ ЩҮШұ ЫҢЪ© ЪҶЩҶШҜ ЩҒШұШіЩҶЪҜ ШұЩҒШӘЩҮ Ш§ЩҶШҜ ЩҲ Ъ©ШҜШ§Щ… ШұЩҲШІ Ш§ЫҢЩҶ ШұШіЩҲЩ„Ш§ЩҶ ШЁЩҮ ЩҮЩ… Щ…ЫҢ ШұШіЩҶШҜШҹ
Щ…Ш«Ш§Щ„ Ш§ЫҢЩҶ ШҙЩ…Ш§Шұ ЪҶЩҶШ§ЩҶ Ш§ШіШӘ Ъ©ЩҮ Ш№ШҜШҜ ШЁШҜШіШӘ ШўЩҲШұЫҢЩ… Ъ©ЩҮ Ш§ЩҲ ШұШ§ Ш«Щ…ЩҶ ЩҲ Ш№ШҙШұ Ш§ЩҶШҜШұ ШЁШ§ШҙШҜШҢ ЩҲ ШўЩҶ ЪҶЩҮЩ„ Ш§ШіШӘ. Ъ©ЩҮ ЩҫЩҶШ¬ШҢ Ш«Щ…ЩҶ Ш§ЩҲ ШЁШ§ШҙШҜ ЩҲ ЪҶЩҮШ§ШұШҢ Ш№ШҙШұ Ш§ЩҲ. ЩҫШі ЩҮШұ ШҜЩҲ ШұШ§ ШЁЩҮ ЩҮЩ… ЪҜШұШҜ ШўЩҲШұЫҢЩ…ШҢ ЩҶЩҮ ШЁШ§ШҙШҜ. ЪҶЩҮЩ„ Ъ©ЩҮ Ш§ШөЩ„ Ш§ШіШӘ ШЁШұ ШўЩҶ ЩҶЩҮ Ъ©ЩҮ Ш¬ШІЩҲШіШӘШҢ ШЁШЁШ®ШҙЫҢЩ…ШҢ ШЁШұЩҒШӘ ЪҶЩҮШ§ШұШҢ ЩҶЩҮ ШЁШі ЪҶЩҮШ§ШұШҢ ЩҲ ЩҶЩҮ Щ…ЩӮШҜШ§Шұ ШўЩҶ Ш§ШіШӘ Ъ©ЩҮ ЩҮШұ ШҜЩҲ ШұШіЩҲЩ„ ШЁЩҮ ЩҮЩ… ШұШіЫҢШҜЩҮ ШЁШ§ШҙЩҶШҜ. ЩҫШі ЪҶЩҮШ§ШұШҢ ШұШ§ ШҜШұ ЩҫЩҶШ¬ Ъ©ЩҮ Ш«Щ…ЩҶ Ш§ЩҲШіШӘ Ш¶ШұШЁ Ъ©ШұШҜЫҢЩ…ШҢ ШЁШұШўЩ…ШҜ ШөШҜ ЩҲ ШҙШөШӘ ЩҒШұШіЩҶЪҜ.В Ш§ЫҢЩҶ ШұЩҒШӘШ§Шұ ШўЩҶ Щ…ШұШҜШіШӘ Ъ©ЩҮ ЩҮШұ ШұЩҲШІ Ш«Щ…ЩҶ ШұШ§ЩҮ ШұЩҒШӘЩҮ Ш§ШіШӘ. ЩҲ Ш«Щ…ЩҶ ЩҮШұ ШұЩҲШІ ЪҶЩҮЩ„ ЩҲ ЩҫЩҶШ¬ ШўЩ…ШҜЩҮ Ш§ШіШӘ ЩҲ Ш№ШҙШұ ШіЫҢ ЩҲ ШҙШҙ. ЩҲ Щ…ЫҢШ§ЩҶ Ш§ЫҢЩҶ ШҙЩҮШұ ЩҲ ШўЩҶ ШҙЩҮШұ ШіЫҢШөШҜ ЩҲ ШҙШөШӘ ЩҒШұШіЩҶЪҜ ШЁШ§ШҙШҜШҢ ЪҶЩҲЩҶ ЩҮШұ ШҜЩҲ ШұЩҒШӘШ§Шұ ШЁЩҮ ЩҮЩ… ШўЩҲШұЫҢЩ….
ШҜШұ Ш§ЫҢЩҶШ¬Ш§ ШҜЩҲ ЩҫШ§ШҜШҙШ§ЩҮ ШҜЩҲ ЩҒШұШіШӘШ§ШҜЩҮ Ш®ЩҲШҜ ШұШ§ Ш§ШІ ШҜЩҲ ШҙЩҮШұ ШЁЩҮ ШіЩҲЫҢ ШҙЩҮШұ ШҜЫҢЪҜШұ Щ…ЫҢ ЩҒШұШіШӘЩҶШҜ. ЫҢЪ©ЫҢ Ш§ШІ ШўЩҶЩҮШ§ ШЁШ§ЫҢШҜ ЩҮШұ ШұЩҲШІ ЫҢЪ© ЩҮШҙШӘЩ… ЩҲ ШҜЫҢЪҜШұЫҢ ЫҢЪ© ШҜЩҮЩ… Щ…ШіШ§ЩҒШӘ Ъ©Щ„ ШЁЫҢЩҶ ШҜЩҲ ШҙЩҮШұ ШұШ§ Ш·ЫҢ Ъ©ЩҶШҜ. ШЁШ§ЫҢШҜ ШӘШ№ЫҢЫҢЩҶ Ъ©ШұШҜ Ъ©ЩҮ Щ…ШіШ§ЩҒШӘ ШЁЫҢЩҶ Ш§ЫҢЩҶ ШҜЩҲ ШҙЩҮШұ ЪҶЩҶШҜ ЩҒШұШіЩҶЪҜ ШЁЩҲШҜЩҮ Ш§ШіШӘ ЩҲ ЩҮШұ Ъ©ШҜШ§Щ… ЪҶЩҮ Щ…ШіШ§ЩҒШӘЫҢ ШұШ§ Ш·ЫҢ Ъ©ШұШҜЩҮ Ш§ЩҶШҜ ЩҲ ЩҫШі Ш§ШІ ЪҶЩҶШҜ ШұЩҲШІ ШЁЩҮ ЩҮЩ…ШҜЫҢЪҜШұ ШұШіЫҢШҜЩҮ Ш§ЩҶШҜ.
ШЁШ§ ЩҒШұШ¶В Ш§ЫҢЩҶ Ъ©ЩҮ ЩҮШұ ШҜЩҲ ЩҒШұШіШӘШ§ШҜЩҮ ШҜШұ ЫҢЪ© ШІЩ…Ш§ЩҶ ШӯШұЪ©ШӘ Ъ©ШұШҜЩҮ ШЁШ§ШҙЩҶШҜ ЩҲ ШҜШұ ЩҲШіШ· ШұШ§ЩҮ ШЁЩҮ ЩҮЩ… ШұШіЫҢШҜЩҮ ШЁШ§ШҙЩҶШҜШҢ ШІЩ…Ш§ЩҶ ШіЩҒШұ Ш¶ШұШЁ ШҜШұ Щ…Ш¬Щ…ЩҲШ№ ШіШұШ№ШӘ ЩҮШ§ ШЁШұШ§ШЁШұ Щ…ШіШ§ЩҒШӘ Ъ©Щ„ ШЁЫҢЩҶ ШҜЩҲ ШҙЩҮШұ Ш®ЩҲШ§ЩҮШҜ ШЁЩҲШҜ. ЫҢШ№ЩҶЫҢ ШІЩ…Ш§ЩҶ ШіЩҒШұ Ш¶ШұШЁ ШҜШұ Щ…Ш¬Щ…ЩҲШ№ ЫҢЪ© ЩҮШҙШӘЩ… ЩҲ ЫҢЪ© ШҜЩҮЩ… ШЁШұШ§ШЁШұ Щ…ШіШ§ЩҒШӘ Ъ©Щ„ Ш®ЩҲШ§ЩҮШҜ ШЁЩҲШҜ . ШЁЩҮ ШҜЫҢЪҜШұ ШіШ®ЩҶ ШҢ ШІЩ…Ш§ЩҶ ШіЩҒШұ ШЁШұШ§ШЁШұ Ш®ЩҲШ§ЩҮШҜ ШЁЩҲШҜ ШЁШ§ ЫҢЪ© ШЁШұ ШұЩҲЫҢ Щ…Ш¬Щ…ЩҲШ№ ЫҢЪ© ЩҮШҙШӘЩ… ЩҲ ЫҢЪ© ШҜЩҮЩ….В Ъ©ЩҲЪҶЪ©ШӘШұЫҢЩҶ Щ…Ш¶ШұШЁ Щ…ШҙШӘШұЪ© ЩҮШҙШӘ ЩҲ ШҜЩҮ Ш№ШҜШҜ Ш¬ЩҮЩ„ ЩҲ Щ…Ш¬Щ…ЩҲШ№ ШөЩҲШұШӘ ЩҮШ§ ШҢ ЪҶЩҮШ§Шұ ШЁЩҮ Ш№Щ„Ш§ЩҲЩҮ ЫҢ ЩҫЩҶШ¬ШҢ ШЁШұШ§ШЁШұ ЩҶЩҮ Ш®ЩҲШ§ЩҮШҜ ШЁЩҲШҜ. ЩҫШі Щ…ШҜШӘ ШіЩҒШұ ШЁШұШ§ШЁШұ ШЁШ§ ЪҶЩҮЩ„ ШӘЩӮШіЫҢЩ… ШЁШұ ЩҶЩҮ ЩҲ ЫҢШ§ ЪҶЩҮШ§Шұ ЩҲ ЪҶЩҮШ§Шұ ЩҶЩҮЩ… ШұЩҲШІ Щ…ЫҢ ШҙЩҲШҜ.
Ш§ЪҜШұ ЩҮШұ ЩҒШұШіШӘШ§ШҜЩҮ ШҜШұ ЩҮШұ ШұЩҲШІ Щ…ЩӮШҜШ§Шұ ШөШӯЫҢШӯЫҢ ЩҒШұШіЩҶЪҜ ШӯШұЪ©ШӘ Ъ©ШұШҜЩҮ ШЁШ§ШҙШҜШҢ ЩҶЩҮ ШұШ§В ШЁШ§ЫҢШҜ ШЁЩҮ ШӘШұШӘЫҢШЁ Ш¶ШұШЁ ШҜШұ ЩҫЩҶШ¬ ЩҲ ЪҶЩҮШ§Шұ Ъ©ЩҶЫҢЩ… ШӘШ§ ШЁЩҮ ШӘШұШӘЫҢШЁ ЪҶЩҮЩ„ ЩҲ ЩҫЩҶШ¬ ЩҲ ШіЫҢ ЩҲ ШҙШҙ ШЁЩҮ ШҜШіШӘ ШўЫҢШҜ Ъ©ЩҮ Щ…ШіШ§ЩҒШӘ Ъ©Щ„ ШұШ§ЩҮЫҢ Ш§ШіШӘ Ъ©ЩҮ ЩҮШұ ШұЩҲШІ ЩҮШұЫҢЪ©ЫҢ Ш§ШІ Ш§ЫҢЩҶ ЩҒШұШіШӘШ§ШҜЩҮ ЩҮШ§ ШұЩҒШӘЩҮ Ш§ЩҶШҜ. Ш§ЫҢЩҶ Ъ©ЩҮ Щ…ЩӮШҜШ§Шұ Ъ©Щ…ШӘШұЫҢЩҶ Щ…ЩӮШҜШ§Шұ ШөШӯЫҢШӯЫҢ Ш§ШіШӘ Ъ©ЩҮ ЩҮШұ Ъ©ШҜШ§Щ… ШҜШұ ЩҮШұ ШұЩҲШІ Ш·ЫҢ Ъ©ШұШҜЩҮ Ш§ЩҶШҜ.В В Ш§ЪҜШұ Ш§ЫҢЩҶ ШҜЩҲ Ш№ШҜШҜ ШЁЩҮ ШҜШіШӘ ШўЩ…ШҜЩҮ (ЫҢШ№ЩҶЫҢ ЪҶЩҮЩ„ ЩҲ ЩҫЩҶШ¬ ЩҲ ШіЫҢ ЩҲ ШҙШҙ) ШұШ§ Ш¶ШұШЁШҜШұ ЩҮШҙШӘ ЩҲ ШҜЩҮ (ШЁШ®ШҙЫҢ Ш§ШІ Щ…ШіШ§ЩҒШӘЫҢ Ъ©ЩҮ ЩҮШұ ШұЩҲШІ Щ…ЫҢ ШұЩҒШӘЩҮ Ш§ЩҶШҜ) ШЁЪ©ЩҶЫҢЩ…ШҢ ЩҒШ§ШөЩ„ЩҮ Ъ©Щ„ ШЁЫҢЩҶ Ш§ЫҢЩҶ ШҜЩҲШҙЩҮШұ ШұШ§ Ъ©ЩҮ ШіЫҢШөШҜ ЩҲ ШҙШөШӘ Ъ©ЫҢЩ„ЩҲЩ…ШӘШұ Ш§ШіШӘ ШЁЩҮ ШҜШіШӘ Щ…ЫҢ ШўЩҲШұЫҢЩ…. Ш§ШІ ШўЩҶШ¬Ш§ЫҢЫҢ Ъ©ЩҮ Ш§ЫҢЩҶ ШҜЩҲ ШЁЩҮ ШіШұШ№ШӘ ЫҢЪ© ЩҮШҙШӘЩ… ЩҲ ЫҢЪ© ШҜЩҮЩ… ШӯШұЪ©ШӘ Щ…ЫҢ Ъ©ШұШҜЩҮ Ш§ЩҶШҜ ЫҢШ№ЩҶЫҢ Ш§ЪҜШұ Ъ©Щ„ ШІЩ…Ш§ЩҶ ЩҮШ¬ШҜЩҮ ШұЩҲШІ ШЁЩҲШҜЩҮ Ш§ШіШӘ ЫҢЪ©ЫҢ Ш§ШІ ШўЩҶЩҮШ§ ЩҮШҙШӘ ШұЩҲШІ ЩҲ ШҜЫҢЪҜШұЫҢ ШҜЩҮ ШұЩҲШІ ШұШ§ЩҮ ШұЩҒШӘЩҮ Ш§ШіШӘ ШЁЩҶШ§ШЁШұШ§ЫҢЩҶВ Щ…ШіЫҢШұ Ш·ЫҢ ШҙШҜЩҮ ШӘЩҲШіШ· ЫҢЪ©ЫҢ ШҜЩҮ ЩҮШ¬ШҜЩҮЩ… ЫҢШ§ ЩҫЩҶШ¬ ЩҶЩҮЩ… Ш§ШіШӘ Ъ©ЩҮ Ш§ЪҜШұ ШўЩҶ ШұШ§ ШҜШұ ШіЫҢШөШҜ ЩҲ ШҙШөШӘ Ш¶ШұШЁ Ъ©ЩҶЫҢЩ… ШөШҜ ЩҲ ШҙШөШӘ ЩҒШұШіЩҶЪҜ ЩҲ Ш§ЪҜШұ ШҜШұ ЩҮШҙШӘ ЩҮШ¬ШҜЩҮЩ… ЫҢШ§ ЪҶЩҮШ§Шұ ЩҶЩҮЩ… Ш¶ШұШЁ Ъ©ЩҶЫҢЩ… Щ…ШіШ§ЩҒШӘ ШҜЩҲЫҢШіШӘ ЩҒШұШіЩҶЪҜ ШұШ§ ШЁЩҮ ШҜШіШӘ Щ…ЫҢ ШўЩҲШұЫҢЩ….
Ш§ЫҢЩҶ Щ…ШіШҰЩ„ЩҮ ШұШ§ Щ…ЫҢ ШӘЩҲШ§ЩҶ ШЁШ§ ЫҢЪ© Щ…Ш№Ш§ШҜЩ„ЩҮ ШіШ§ШҜЩҮ ШӯЩ„ Ъ©ШұШҜ: Ш§ЪҜШұ ЩҒШ§ШөЩ„ЩҮ ШҜЩҲ ШҙЩҮШұ ШұШ§ xВ ЩҒШұШ¶ Ъ©ЩҶЫҢЩ…ШҢ Щ…ШіШ§ЩҒШӘЫҢ Ъ©ЩҮ ЩҫЫҢЪ© Ш§ЩҲЩ„ Ш·ЫҢ Щ…ЫҢ Ъ©ЩҶШҜВ В a ЩҲ ЩҫЫҢЪ© ШҜЩҲЩ… b . ЩҫШі:
x=a+b
ШіШұШ№ШӘ ЩҮШұ ЩҫЫҢЪ© ШұШ§ ЩҮЩ… ЩҫШ§ШҜШҙШ§ЩҮШ§ЩҶ Щ…ШҙШ®Шө Ъ©ШұШҜЩҶШҜ (v1В ЩҲВ В v2 ШіШұШ№ШӘВ ЩҮШұЫҢЪ© Ш§ШІ ШўЩҶЩҮШ§ Ш§ШіШӘ):
v1=x/8В В В В В В В В
v2=x/10В В В
t
ШІЩ…Ш§ЩҶ Ш§ШіШӘ ЩҲ Ш·ШЁЩӮ ШіШ§ШҜЩҮ ШӘШұЫҢЩҶ ЩҒШұЩ…ЩҲЩ„ ШҜЫҢЩҶШ§Щ…ЫҢЪ© ШЁШ§ ЩҒШұШ¶ Ш§ЫҢЩҶ Ъ©ЩҮ ШҙШӘШ§ШЁ ШӯШұЪ©ШӘ Ш§ЫҢЩҶ Ш§ЩҒШұШ§ШҜ ШөЩҒШұ ШЁШ§ШҙШҜ:
a=v1*t Гһ t=8a/x
b=v2*t Гһ t=10b/x
ЩҲЩӮШӘЫҢ Ъ©ЩҮ Ш§ЫҢЩҶ ШҜЩҲ ЩҫЫҢЪ© ШЁЩҮ ЩҮЩ… Щ…ЫҢ ШұШіЩҶШҜШҢ ШІЩ…Ш§ЩҶ Щ…ШіШ§ЩҲЫҢ ШұШ§ Ш·ЫҢ Ъ©ШұШҜЩҮ Ш§ЩҶШҜ:
8a/x=10b/x Гһ b= (8/10) * a
Ш§ШІ Ш§ЩҲЩ„ЫҢЩҶ ЩҒШұЩ…ЩҲЩ„ ЩҮЩ… ШҜШ§ШҙШӘЫҢЩ… Ъ©ЩҮ:
x=a+b Гһ x=a+(8/10)*a Гһ x= (18/10) * a
ШӯШ§Щ„Ш§ Щ…Ш§ ШӘЩ…Ш§Щ… Щ…ЩӮШҜШ§ШұЩҮШ§ ШұШ§ ШҜШ§ШұЫҢЩ… ЩҲ Ъ©Ш§ЩҒЫҢ Ш§ШіШӘ Ъ©ЩҮ ЩҒШ§ШөЩ„ЩҮ ШҜЩҲ ШҙЩҮШұ ШұШ§ ЫҢЪ© Ш№ШҜШҜ ЩҒШұШ¶ЫҢ ШЁЪҜЫҢШұЫҢЩ…ШҢ ШЁШ§ЩӮЫҢ ЩӮШ§ШЁЩ„ Щ…ШӯШ§ШіШЁЩҮ Ш®ЩҲШ§ЩҮЩҶШҜ ШЁЩҲШҜ.
Ъ©Ш§ШұЫҢ Ъ©ЩҮ ШҜШұ Щ…Ш«Ш§Щ„ Ш®ЩҲШҜШҙ Ш§ЩҶШ¬Ш§Щ… ШҜШ§ШҜЩҮ ШіШ№ЫҢ Ъ©ШұШҜЩҮ Ш№ШҜШҜЩҮШ§ЫҢЫҢ ШұШ§ ЩҒШұШ¶ Ъ©ЩҶШҜ Ъ©ЩҮ Ш¬ЩҲШ§ШЁЩҮШ§ЫҢ ШұЩҶШҜ ЩҲ ШЁШҜЩҲЩҶ Ш§Ш№ШҙШ§Шұ ШЁШҜШіШӘ ШЁЫҢШ§ЩҲШұШҜ.
Щ…Ш«Щ„Ш§ ШҜШұ Ш§ЩҲЩ„ЫҢЩҶ ЩҒШұЩ…ЩҲЩ„ ШЁШ§Щ„Ш§ b=(8/10)*aВ Ъ©ЩҲЪҶЪ©ШӘШұЫҢЩҶ Щ…Ш¶ШұШЁ Щ…ШҙШӘШұЪ© 8В ЩҲВ 10 ШЁШұШ§ШЁШұ 40В Ш§ШіШӘ Ъ©ЩҮ Ш§ШІ ЩҮЩ…ЫҢЩҶ Ш§ШіШӘЩҒШ§ШҜЩҮ Ъ©ШұШҜЩҮ Ш§ШіШӘ.
ШҜШұ Щ…Ш«Ш§Щ„ Ш·ШЁШұЫҢВ a ШЁШұШ§ШЁШұВ 160 ЩҒШұШіЩҶЪҜ ЩҲВ b ШЁШұШ§ШЁШұ 200В ЩҒШұШіЩҶЪҜ ЩҲ Ш¬Щ…Ш№ ШўЩҶЩҮШ§ 360В ЩҒШұШіЩҶЪҜ Щ…ЫҢ ШҙЩҲШҜ.
ЩҫЫҢвҖҢЩҶЩҲШҙШӘвҖҢЩҮШ§:
*ЩҶЩҲЫҢШіЩҶШҜЩҮ ШҜШұ ШӯЩ„ Щ…ШіШ§ЫҢЩ„ Ш§ЫҢЩҶ Ъ©ШӘШ§ШЁ Ш§ШІ Щ…ШҙЩҲШұШӘ ЩҲ ЫҢШ§ШұЫҢ ШўЩӮШ§ЫҢ Щ…ЩҮЩҶШҜШі Ш§ШӯЩ…ШҜШұШ¶Ш§ ШӘЩҲЪ©Щ„ЫҢ ШөШ§ШЁШұЫҢ ЩҲ ЩҫЩҲЫҢШ§ ШӘЩҲЪ©Щ„ЫҢ ШөШ§ШЁШұЫҢ ШЁЩҮШұЩҮ ШЁШұШҜЩҮ Ш§ШіШӘ Ъ©ЩҮ ШҜШұ Ш§ЫҢЩҶШ¬Ш§ Ш§ШІ Ш§ЫҢШҙШ§ЩҶ ШіЩҫШ§ШіЪҜШІШ§ШұЫҢ Щ…ЫҢ Ъ©ЩҶШҜ.





